Республиканская олимпиада по математике, 2023 год, 10 класс
Комментарий/решение:
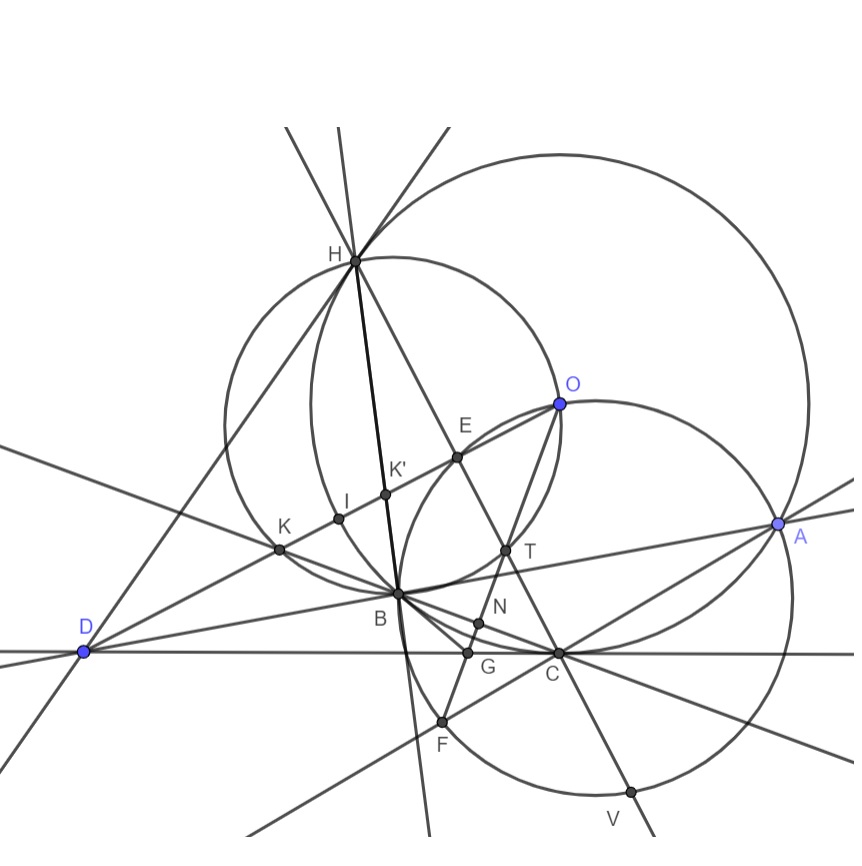
Заметим, что при инверсии относительно $\omega$ прямая $AB$ переходит в $\Omega$ и наоборот, значит $D$ и $E$ переходят друг в друга. Тогда $T'$ - образ точки $T$ лежит на прямой $OF$ и на описанной окружности треугольника $OCD$. Поскольку $OC$ - радиус, а $CD$ - касательная, то $\angle BCD = \angle BAC$ и $OC \perp CD$. Тогда, $\angle OTD = \angle OCD = 90 ^\circ$. Поскольку $O,A,F,B \in \Omega$, то $ \angle BOF = \angle BAF = \angle BAC = \frac{\angle BOC}{2} $. Значит, $OT'$ - биссектриса в равнобедренном $\triangle BOC$. Заметим, что $K'$ - образ точки $K$ лежит на описанной окружности $ \triangle BOC$ и прямой $OD$. Пусть, $G$ - диаметрально противоположна $O$ на описанной окружности $ \triangle BOC$. Тогда, $\angle BCG=\angle BOG = \frac{\angle BOC}{2} = \angle BCD$. Значит, $D = CG \cap OK'$. Поскольку $\triangle BOC$ - равнобедренный, то касательная к $O$ параллельна $BC$. Значит, применяя теорему Паскаля к $OOK'BCG$ мы получаем, что $OO \cap BC = \infty_{BC}$, $OK' \cap CG =D$ и $BK' \cap OG$ лежат на одной прямой. С другой стороны, $T' = D \infty_{BC} \cap OG$, значит $T'$ - это и есть наша третья точка, то есть $T',B,K'$ коллинеарны. Но тогда их образы вместе с центром инверсии лежат на одной окружности, то есть точки $O,B,T,K$ на одной окружности. $\square$
Проведем так же вторую касательную $DH$ к $\omega$ из точки $D$ пусть $E$' середина $CH$ тогда $DC^2=DE' \cdot DO = DB \cdot DA$ то есть $DA$ образ окружности $\Omega$ при инверсии $\omega$, то есть $E'=E$. Так как $OB=OA$ откуда $FO$ биссектриса $\angle BFC$ тогда $FO \perp BC$ пусть $N \in BC \cap FO$ тогда $\angle CNO = \angle CEO$ или $CNEO$ $(1)$ лежат на одной окружности, так как $DO$ биссектриса равнобедренного треугольника $DHC$ тогда $\angle KCH = \angle KHC$ но из $(1)$ получается $\angle KCH = \angle KOF$ то есть $KHOTB$ лежат на одной окружности

Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.