Областная олимпиада по математике, 1999 год, 11 класс
Полные решения этих задач опубликованы в книге, доступный для заказа по ссылке
Задача №1. Докажите неравенство $1^1 \cdot 2^2 \cdot 3^3 \cdot \dots \cdot 1998^{1998} > (1998!)^{\tfrac{{1999}}
{2}} $.
комментарий/решение(5)
комментарий/решение(5)
Задача №2. Пусть $a_1$ и $a_2$ произвольные цифры. Для каждого натурального $n$ последнюю цифру числа $19a_{n+1}+99a_n$ в его десятичной записи обозначим через $a_{n+2}$. Докажите, что число $0,a_1a_2a_3 \dots $ — рациональное.
комментарий/решение(1)
комментарий/решение(1)
Задача №3. Найдите все такие функции $f: \mathbb{R} \to \mathbb{R} $, удовлетворяющих соотношениям: $f(xf(x) + f(y)) = f^2 (x) + y$ и $f(0)=0.$
комментарий/решение(2)
комментарий/решение(2)
Задача №4. Пусть $ABC$ — остроугольный треугольник, $H$ — его ортоцентр. Обозначим через $M$ середину отрезка $BH$, а через $N$ проекцию точки $H$ на биссектрису внутреннего угла $B$. докажите, что прямая $MN$ делит сторону $AC$ пополам.
комментарий/решение(1)
комментарий/решение(1)
Задача №5. Найдите все вещественные значения $a$, такие что уравнение $x^8+ax^4+1=0$ имеет четыре корня, образующие арифметическую прогрессию.
комментарий/решение(1)
комментарий/решение(1)
Задача №6. Можно ли без наложения замостить доску размером $99\times 99$ плитками вида
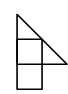 и
и
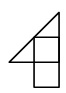 ?
?
комментарий/решение(1)
комментарий/решение(1)
Задача №7. В квадрате $ABCD$ расположена точка $P$ таким образом, что $AP=2\sqrt3$; $BP=\sqrt2$; $CP=4$. Докажите, что $\angle APC = 120^\circ $.
комментарий/решение(1)
комментарий/решение(1)
Задача №8. Число 2211 представлено в виде суммы двадцати трех целых положительных чисел. Какое наименьшее возможное значение наименьшего общего кратного этих двадцати трех чисел?
комментарий/решение(2)
комментарий/решение(2)