Математикадан облыстық олимпиада, 1998-1999 оқу жылы, 11 сынып
Полные решения этих задач опубликованы в книге, доступный для заказа по ссылке
Есеп №1. Келесі теңсіздікті дәлелдеңіз: ${{1}^{1}}\cdot {{2}^{2}}\cdot {{3}^{3}}\cdot \ldots \cdot {{1998}^{1998}} > {{(1998!)}^{\tfrac{1999}{2}}}$.
комментарий/решение(5)
комментарий/решение(5)
Есеп №2. ${{a}_{1}}$ және ${{a}_{2}}$ кез келген цифрлар болсын. Әрбір натурал $n$ үшін ${{a}_{n+2}}$ арқылы $19{{a}_{n+1}}+99{{a}_{n}}$ санының ондық сандар жүйесіндегі соңғы цифрын белгілейік. Онда $0,{{a}_{1}}{{a}_{2}}{{a}_{3}}\ldots $ санының рационал екенін делелде.
комментарий/решение(1)
комментарий/решение(1)
Есеп №3. Келесі теңдіктерді қанағаттандыратын барлық $f:\mathbb{R}\to \mathbb{R}$ функцияларын тап: $f\left( xf\left( x \right)+f\left( y \right) \right)={{f}^{2}}\left( x \right)+y$ және $f\left( 0 \right)=0$.
комментарий/решение(2)
комментарий/решение(2)
Есеп №4. $ABC$ — сүйір бұрышты үшбұрыш, $H$ — оның ортоцентрі. $BH$ кесіндісінің ортасын $M$ арқылы белгілейік, ал $N$ нүктесі $H$ нүктесінің $B$ ішкі бұрышының биссектрисасындағы проекциясы, $MN$ түзуі $AC$ қабырғасын қақ бөлетінін далелдеңіз.
комментарий/решение(2)
комментарий/решение(2)
Есеп №5. ${{x}^{8}}+a{{x}^{4}}+1=0$ теңдеуінің төрт түбірі арифметикалық прогрсссия кұрайтындай $a$-ның барлық мәнін тап.
комментарий/решение(1)
комментарий/решение(1)
Есеп №6. Сурегге көрсетілген «бір» тәріздес плиткаларымен бір-бірімен қиылыспайтындай етіп $99\times 99$ шақпақты тақтаныжауып шығуга бола ма;
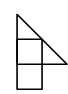 және
және
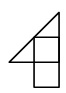 ?
?
комментарий/решение(1)
комментарий/решение(1)
Есеп №7. $ABCD$ квадратының ішінде $P$ нүктесі $AP=2\sqrt{3}$; $BP=\sqrt{2}$; $PC=4$ болатындай орналасқан. $\angle APC=120{}^\circ $ екенін дәлелдеңіз.
комментарий/решение(1)
комментарий/решение(1)
Есеп №8. 2211 сан жиырма үш натурал санның косындысы түрінде жазылған. Осы жиырма үш санның ең кіші ортақ еселігі $A$ болсын. $A$-ның ең кіші мүмкін мәнін тап.
комментарий/решение(2)
комментарий/решение(2)