6-я международная Иранская олимпиада по геометрии, 2019 год, первая лига, 7-8 классы

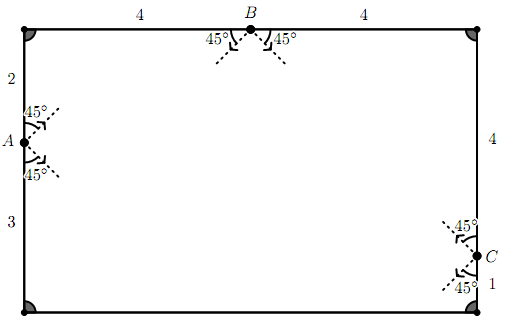
Задача №1. Дан прямоугольный стол размером $8 \times 5$, в углах которого расположены лунки. Шар по очереди запускают из точек $A$, $B$ и $C$ в шести указанных на рисунке направлениях. В каких случаях шар попадёт в одну из лунок после не более чем 6 отражений? (Шар отражается от сторон прямоугольника по закону <<угол падения равен углу отражения>>.)

комментарий/решение

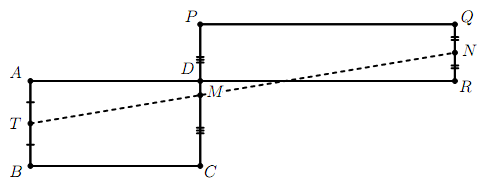
Задача №2. Два прямоугольника $ABCD$ и $PQRD$ одинаковой площади, соответствующие стороны которых параллельны, расположены, как показано на рисунке. Точки $N$, $M$ и $T$ — середины отрезков $QR$, $PC$ и $AB$ соответственно. Докажите, что точки $N$, $M$ и $T$ лежат на одной прямой.

комментарий/решение(2)

Задача №3. На плоскости проведены $n>2$ прямых общего положения, то есть никакие две прямые не параллельны и никакие три прямые не проходят через одну точку. Точки пересечения этих прямых отметили, после чего все прямые стёрли, оставив при этом отмеченные точки. Неизвестно, каким двум прямым принадлежит каждая из отмеченных точек. Можно ли однозначно узнать, какая точка какой прямой принадлежит, и восстановить исходные прямые?
комментарий/решение(1)

Задача №4. Дан четырёхугольник $ABCD$ такой, что $\angle DAC = \angle CAB = 60^\circ \quad AB = BD - AC.$ Обозначим через $E$ точку пересечения прямых $AB$ и $CD$. Докажите, что $\angle ADB = 2\angle BEC$.
комментарий/решение(1)

Задача №5. Назовём диагональ выпуклого многоугольника (т.е. многоугольника, все углы которого меньше $180^\circ$) срединной, если она делит пополам и площадь, и периметр многоугольника. Какое наибольшее число срединных диагоналей может быть у выпуклого пятиугольника?
комментарий/решение(1)