А. Антропов
Есеп №1. $9 \times 9$ тор көзді тақтаға ең көп дегенде бір бірін жемейтіндей(сондай ақ, өзінің түсімен бірдей пешканы) қанша қара және ақ пешка қоюға (пешка, өзінің түсіне тәуелсіз кез келген шаршыға қоюға болады) болады? Ақ пешка нөмері үлкен көршіес екі диоганальді жейді, ал қара пешка нөмері төмен екі көршілес диоганальді жейді (сур. қараңыз).
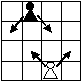
комментарий/решение(1) олимпиада
Есеп №2. $ABC$ үшбұрышының $AB$ қабырғасы $BC$ қабырғасынан үлкен. $BC$ қабырғасының $C$ нүктесінен әрі қарай созындысынан $2BN=AB+BC$ болатындай $N$ нүктесін белгілеген. $BS$ — $ABC$ үшбұрышының биссектрисасы, $M$ — $AC$ қабырғасының ортасы, ал $L$ нүктесі $BS$ кесіндісіндегі $ML \parallel AB$ болатындай нүкте. $2LN=AC$ екенін дәлелдеңіздер. ( А. Антропов )
комментарий/решение(8) олимпиада
Есеп №3. а стороне $AB$ треугольника $ABC$ выбрана точка $P$, а на сторонах $AC$ и $BC$ точки $S$ и $T$ таким образом, что $AP=AS$ и $BP=BT$. Описанная окружность треугольника $PST$ вторично пересекает стороны $AB$ и $BC$ в точках $Q$ и $R$ соответственно. Прямые $PS$ и $QR$ пересекаются в точке $L$. Докажите, что прямая $CL$ делит отрезок $PQ$ пополам. ( А. Антропов )
комментарий/решение(1) олимпиада
Есеп №4. Серёжа мен Таня Машаға мынадай фокус көрсетпекші. Серёжа бөлмеден шығып кетеді. Маша $a_1,a_2,\ldots,a_n$ тізбегін жазады, мұнда әр $a_k$ саны 0 немесе 1-ге тең. Сосын Таня $b_1,b_2,\ldots,b_n$ де 0 немесе 1-ден құралған тізбек жазады. Осыдан кейін Маша не ештеңе істемейді, не «Мутабор!» деп айтып, екі тізбекті де ауыстырады: өзінікін — кері ретпен $a_n,a_{n-1},\ldots,a_1$, ал Таняның тізбегін — $1-b_n,1-b_{n-1},\ldots,1-b_1$. Маша өз тізбегін майлықпен жабады, Серёжа қайта кіреді. Серёжа Таняның тізбегіне қарап, майлықтың астындағы тізбекті атауы тиіс. Қай $n$ үшін Серёжа мен Таня алдын ала дайындалып, мұндай фокусты көрсете алады? Серёжа «Мутабор» жасалды ма, соны анықтауға міндетті емес. ( А. Антропов, Т. Гизатуллин )
комментарий/решение олимпиада
Есеп №5. $ABC$ үшбұрышы ішінде $L$ нүктесі үшін $CL=AB$ және $\angle BAC+\angle BLC=180^\circ$ теңдіктері орындалады. $BC$ түзуіне параллель және $L$ нүктесі арқылы өтетін түзу $AC$ қабырғасын $K$ нүктесінде қиып өтеді. $AB=BK$ екенін дәлелдеңіз. ( А. Антропов )
комментарий/решение(1) олимпиада