Математикадан республикалық олимпиада, 2015-2016 оқу жылы, 9 сынып

$ABC$ үшбұрышына сырттай $\omega$ шеңбер сызылған, ал $I$ нүктесі — осы үшбұрыштың биссектрисаларының қиылысу нүктесі. $CI$ түзуі $\omega$-ны екінші рет $P$ нүктесінде қияды. Диаметрі $IP$ болатын шеңбер, $AI$, $BI$ және $\omega$-ны екінші рет сәйкесінше $M$, $N$ және $K$ нүктелерінде қияды. $KN$ және $AB$ кесінділері $B_1$, ал $KM$ және $AB$ кесінділері $A_1$ нүктесінде қиылыссын. $\angle ACB = \angle A_1IB_1$ теңдігін дәлелдеңіз. ( М. Кунгожин )

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.     По лемме трезубца $PA=PI=PB$. Поэтому $M$ и $N$ середины отрезков $AI$ и $BI$ соответственно. Пусть $Q$ — середина дуги $ACB$ описанной окружности $\triangle ABC$. Если провести окружность с центром в точке $P$ радиусом $PI$, то прямые $QA$ и $QB$ будут касаться этой окружности. Пусть точка $J$ — симметрична точке $I$ относительно $K$. Тогда $J$ лежит на рассматриваемой окружности. Обозначим $KM \cap AQ=L$. Тогда $\angle IKL = \angle IJA = \angle IAL$. Следовательно, четырехугольник $ALIK$ вписанный. Имеем: $\angle ILQ = \angle AKQ = \angle ABQ = \angle BAQ$, то есть $IL \parallel AB$, откуда немедленно следует, что $ALIA_1$ — параллелограмм. Значит, $\angle A_1IK = \angle AQK$. Аналогично, $\angle B_1IK= \angle BQK$. Поэтому $\angle A_1IB_1 = \angle AQB = \angle ACB$.

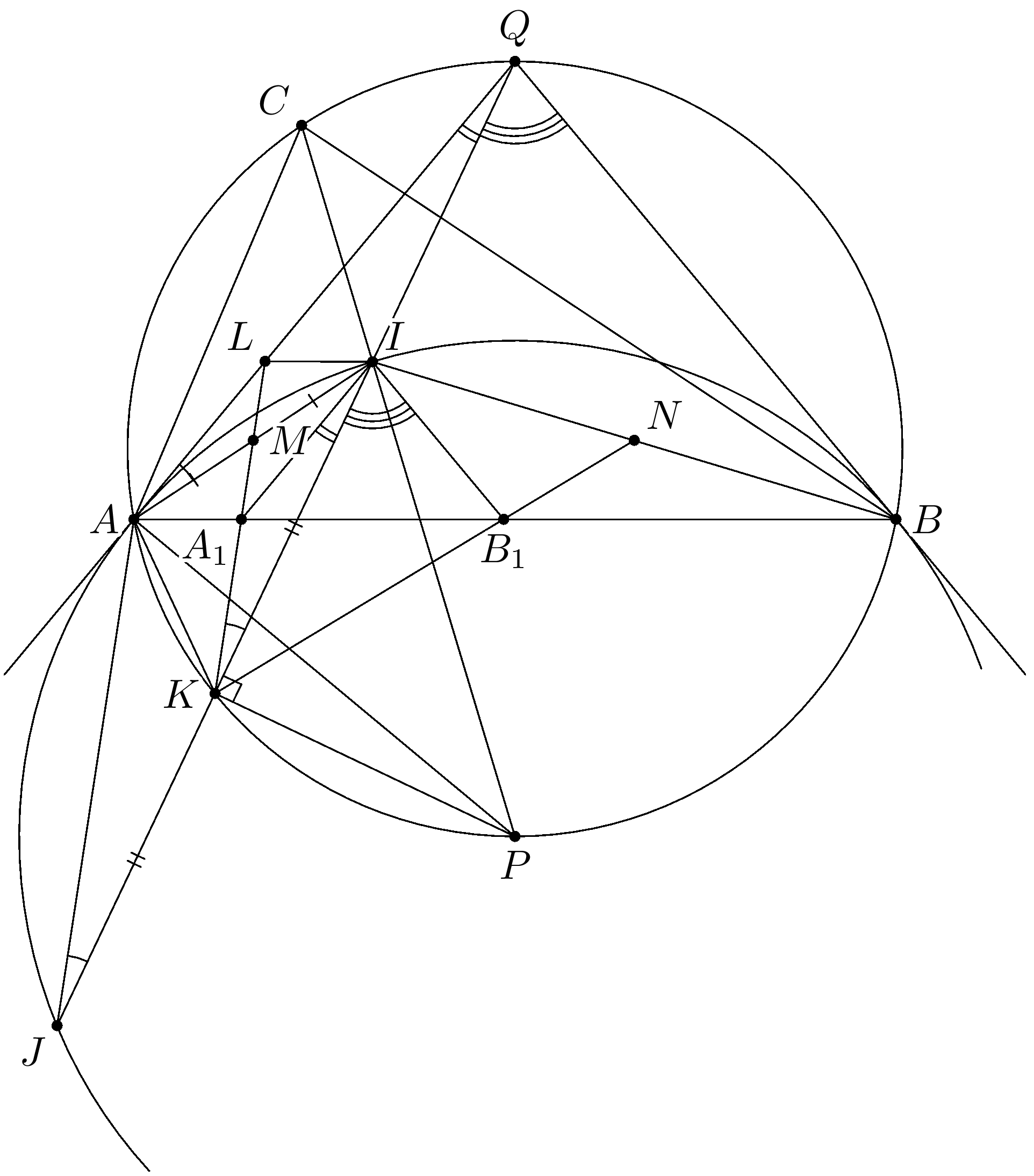
По лемме о трезубце $$PA=PI=PB$$

из условия $PM\bot AI$ откуда $$\angle IPM=\frac{\angle IPA}{2}=\frac{\angle ABC}{2}=\angle ABI=\angle A_1BI$$ из того, что $IMKP$- вписанный следует,что $$\angle IKA_1=\angle IKM=\angle IPM$$ поэтому $$\angle IKA_1=\angle IBA_1$$

откуда $IBKA_1$- вписанный, следовательно $$\angle A_1IK=\angle A_1BK$$ аналогично $$\angle B_1IK=\angle B_1AK$$

из двух последних равенств получаем, что $$\angle A_1IB_1=\angle B_1AK+\angle A_1BK=\angle ACB$$

Понятно что K;I;T на одной прямой где T середина большей дуги так же понятно что M и N середины BI;CI.Тогда возьмем фантом поинт B1

B1 на отрезке BC так что ICBB1 вписанный и пусть U середина BC.Тогда из леммы область 2009 ATI=IKB => Пусть CBA= 2b и CAB=2a => IA1A=b+a => BIB1=a => BIB1 и BIA подобны так же MB1I=PAI=IUB-a => AMB=IUB но тк такая точка на отрезке единственная => M середина BI значит наш фантом поинт совпадет с B1 из условия и так де BIA1=a аналогично AIA1 = b значит A1IB1= 180-2a-2b=BAC