XVII математическая олимпиада «Шелковый путь», 2018 год

В остроугольном треугольнике $ABC$ на сторонах $AB$, $BC$, $AC$ соответственно взяты точки $H$, $L$, $K$ так, что $CH \perp AB$, $HL \parallel AC$, $HK \parallel BC$. Пусть $P$ и $Q$ — основания высот треугольника $HBL$, проведенные из вершин $H$ и $B$ соответственно. Докажите, что основания высот треугольника $AKH$, проведенные из вершин $A$ и $H$, лежат на прямой $PQ$. ( М. Кунгожин )

Комментарий/решение

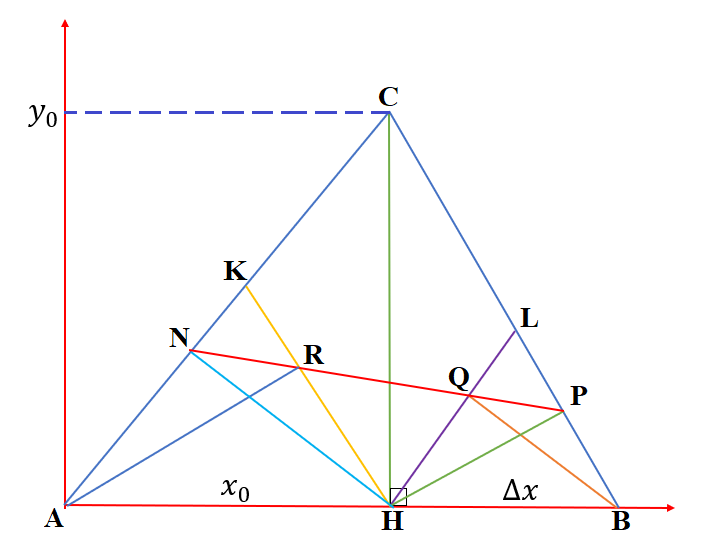
$$ CH \bot AB, \quad HP \bot BC , \quad HN\bot AC, \quad AR \bot KH, \quad BQ \bot LH$$

$$ A(0;0), \quad H(x_0;0) , \quad B(x_0+\Delta x;0),\quad C(x_0;y_0)$$

$$ CH: y=x_0, \qquad AC: y =\frac{y_0}{x_0}\cdot x$$

$$ BC: y=-\frac{y_0}{\Delta x}\cdot x+y_0 \left(1+\frac{x_0}{\Delta x}\right)$$

$$HL: y=\frac{y_0}{x_0}(x-x_0), \qquad KH: y=\frac{y_0}{\Delta x}(x_0-x)$$

$$ HP: y=\frac{\Delta x}{y_0}(x-x_0), \qquad BQ: y=\frac{x_0}{y_0}(x_0+\Delta x-x)$$

$$ AR: y=\frac{\Delta x}{y_0}\cdot x, \qquad HN: y = \frac{x_0}{y_0}(x_0-x)$$

$$ P=HP\cap BC \Rightarrow P\left(x_0+\frac{y^2_0 \Delta x}{\Delta x^2+y^2_0};\frac{ y_0 \Delta x^2}{\Delta x^2+y^2_0} \right)$$

$$ Q= HL\cap BQ \Rightarrow Q\left(x_0+\frac{x^2_0 \Delta x}{ x^2_0+y^2_0};\frac{ y_0 x_0\Delta x}{ x^2_0+y^2_0} \right)$$

$$ R=KH \cup AR\Rightarrow R\left(\frac{x_0 y^2_0}{\Delta x^2+y^2_0};\frac{ y_0 x_0\Delta x}{\Delta x^2+y^2_0} \right)$$

$$ N= HN\cap AC \Rightarrow N\left(\frac{x^3_0}{ x^2_0+y^2_0};\frac{ x_0^2 y_0}{ x^2_0+y^2_0} \right)$$

$$QN: y=\frac{y_0}{y^2_0+x_0\Delta x} (x(\Delta x-x_0)-x_0^2)$$

$$ PR: y=\frac{y_0}{y^2_0+x_0\Delta x} (x(\Delta x-x_0)-x_0^2)$$

$$ \Rightarrow y_{PR}=y_{QR} \Rightarrow P,Q,R \in l$$

$N \in AC,R \in HK$ основания высот треугольника $AKH$ , пусть $NR$ пересекает $CH$ В $X$ , тогда $\angle CHN= \angle BAC$ и $\angle HNR= \angle HAR = 90^{\circ}-\angle ABC$ откуда $\angle NXH = 90^{\circ}+\angle ABC - \angle BAC$ , пусть $Y \in PQ \cap CH$ аналогично $\angle PYH = 90^{\circ} + \angle BAC - \angle ABC $ откуда $\angle NXH + \angle PYH = 180^{\circ}$ $(1)$ .

По теореме Менелая $\dfrac{CX}{HX} = \dfrac{NC}{NK} \cdot \dfrac{RK}{RH} , \ \ \dfrac{CY}{HY} = \dfrac{PC}{PL} \cdot \dfrac{QL}{QH}$ учитывая параллельность в условий, выражая через углы, получаем $\dfrac{CX}{HX} = \dfrac{CY}{HY} = tgA \cdot tgB$ то есть $X=Y$ и учитывая $(1)$ получается $A, H \in PQ$

NR может быть параллельно PQ.

Пусть $LK$ пересекает $AB$ в точке $X$. Достаточно доказать что $P, Q, X$ лежат на одной прямой. Обозначим пересечение $XQ$ и $AC$ как $D$. Из за гомотетии $HD$ перпендикулярен $AC$. Очевидно что, $AB$ касательная к окружности описанной около $P, H, D, C$. Отметим точку пересечение $XQ$ с окружностью ($P, H, D, C$) как $P1$ тогда из за того что $AB$ касательная к ($P, H, D, C$) угл $\angle P1DH=\angle P1HB$. С другой стороны $\angle P1DH=\angle P1QB$ из за гомотетии. Значит $P1$ лежит на окружности описанной около ($B, H, Q$). Это означает что у окружностей ($B, H, Q$) и ($P, H, D, C$) есть три точки пересечение что невозможно значит $P1=P$. Из чего следует что $P, Q, X$ лежат на одной прямой. Значит основание высот в треугольнике $\triangle AKH$ также будут лежать на прямой $P, Q, X$ из за гомотетии.

Пиши на латехе брат

Подземелья dungeon так и не открыли?(

Пусть $KL \cap AB = X$ ( Если $KL \parallel AB$ то там все очевидно).

Пусть высоты из точек $A, H$ на стороны треугольника $AKH$ будут $P_1, Q_1$ соответственно.

Заметим:

$\dfrac{XA}{XH}= \dfrac{XK}{XL} = \dfrac{XH}{XB}$.

Рассмотрим гомотетию в точке $X$, переводящую точку $A$ в точку $H$. При такой гомотетии $Q_1 -> Q, P_1 -> P => X - Q_1 - Q, X - P_1 - P$.

Осталось доказать $X - Q_1 - P_1$.

Пусть $R_1-$ основание перпендикуляра из $K$ на $AH$, также $X_1 = P_1Q_1 \cap AB$. В таком случае нам надо доказать $X_1 = X$.

Заметим прямая $XK$ проходит через середину $CH$, т.к $CKHL-$ параллелограмм. Тогда нам требуется того, что $X_1K$ проходит через середину $CH$.

Пусть $X_1K \cap CH = J$. Заметим $-1 = (X_1, R_1 ; A, H) = (KR_1, KJ ; KC, KH)$, так как $KR_1 \parallel CH => CJ=JH$, что и требовалось $\square$

Пусть $AR,HN$-высоты $\triangle KAH$.Тогда $\angle CNR=\angle KNR=180^\circ-\angle RNA=\angle AHR=\angle ABC=\angle HBC=90^\circ-\angle BCH=\angle CHP=\angle CNP\Rightarrow N—R—P$.Аналогично $N—R—Q$