Республиканская олимпиада по математике, 2020 год, 11 класс

На медиане $CM$ треугольника $ABC$ отмечена точка $N$ так, что $MN \cdot MC = AB^2/4$. Прямые $AN$ и $BN$ вторично пересекают описанную окружность $\triangle ABC$ в точках $P$ и $Q$, соответственно. $R$ — точка отрезка $PQ$, ближайшая к $Q$, такая что $\angle NRC = \angle BNC$; $S$ — точка отрезка $PQ$, ближайшая к $P$, такая что $\angle NSC = \angle ANC$. Докажите, что $RN = SN$. ( М. Кунгожин )

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.     Опустим перпендикуляры $AH$ и $BT$ на прямые $BN$ и $AN$ соответственно. Тогда $MA = MB = MH = MT$ и $MN \cdot MC = \dfrac{AB^2}{4} = BM^2 = MH^2$, то есть описанная окружность $\triangle CNH$ касается прямой $MH$ или $\angle HCN = \angle MHN$. Получается, что $\angle HCN = \angle MHN = \angle MBN = \angle BCN$, $\angle HMC = \angle HNC - \angle MHN = \angle HNC - \angle NCB = \angle NBC$ или $\triangle CHM \sim \triangle CNB$.

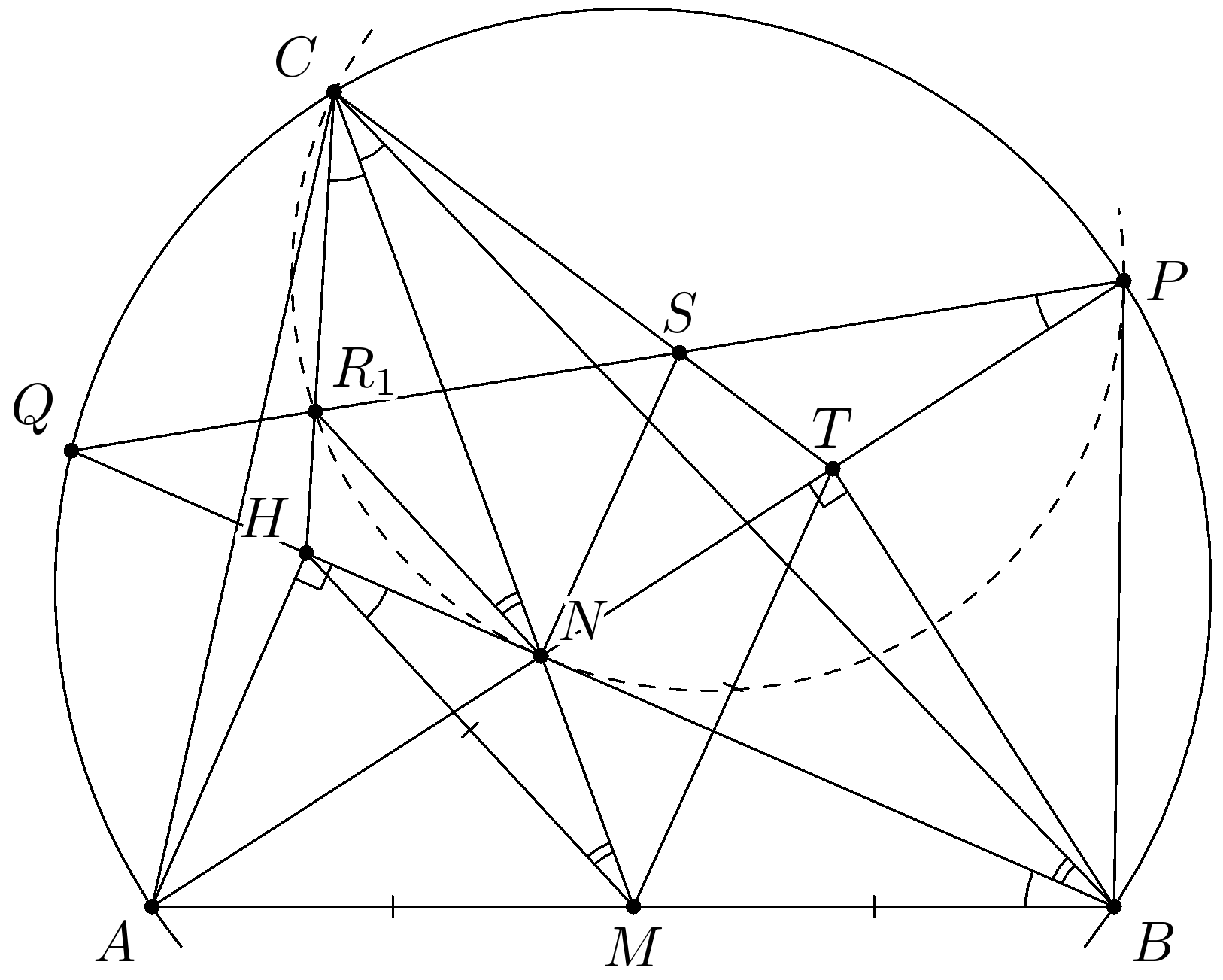
Решение: Из условия $MN\cdot MC = AB^2 / 4=AM^2$ следует, что

$$\angle CQB = \angle CAM = \angle ANM = 180 - \angle ANC = 180 - \angle NSC,$$

значит $CQNS$ вписанный. Тогда $\angle NSR = \angle NCQ = \angle ACB.$ Последнее равенство следует из равенства $\angle MCB = \angle MBN.$

Аналогично $\angle NRS = \angle ACB.$ Отсюда легко вывести требуемое.