Городская Жаутыковская олимпиада по математике, 7 класс, 2025 год

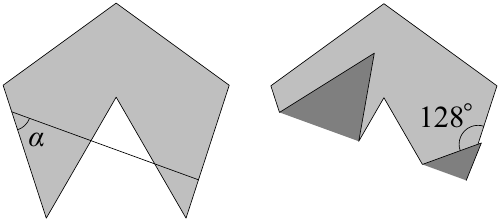
Қағаздан жасалған дұрыс бесбұрыштан дұрыс үшбұрыш қиып алынды (үшбұрыштың екі төбесі бесбұрыштың екі төбесімен сәйкес келеді). Кейін қағазды $\alpha$ бұрышымен көлбеу түзу бойымен бүгіп, бүгілу нәтижесінде $128^\circ$ бұрышы пайда болды. $\alpha$ бұрышын табыңыз.

Комментарий/решение

Назовем вершины пятиугольника как ABCDE начиная с левой нижней вершины треугольника, назовем верхнюю вершину треугольника как F, у нас получился правильный пятиугольник ABCDE и правильный треугольник ABF, вершина с углом а на стороне AE назовем P и вершину у стороны AF - K, BF - T, BC-M а также назовем вершину которой касается треугольник TBM когда его согнули S

$a+128+128+\angle PMB=360 \Rightarrow \angle PMB=104-a$

$\angle TMB=68(128-60) \Rightarrow 68+104-a+\angle BTM=180 \Rightarrow \angle BTM=8+a$

$\angle BTM=\angle MTS$ так как если согнуть треугольник то прилежащие углы будут равны

$\angle TMS=76+a(180-(104-a));\angle TSM=52(180-128)\Rightarrow 8+a+76+a+52=180 \Rightarrow 2a=44 \Rightarrow a=22 $