Городская Жаутыковская олимпиада по математике, 7 класс, 2025 год
Задача №1. 1 рыцарь и 100 лжецов встали в один ряд и спрятали от дежурного его телефон. После этого каждый сказал: «Телефон взял один из моих соседей». Может ли дежурный, задав вопрос только одному стоящему в ряду «Ты ли взял мой телефон?», и получив на него ответ, безошибочно найти, у кого находится его телефон? (Рыцарь говорит только правду, а лжецы — только ложь.)
комментарий/решение(1)
комментарий/решение(1)
Задача №2. Сумма десяти натуральных чисел равна 2025. Какое наибольшее значение может принимать наибольший общий делитель всех этих десяти чисел?
комментарий/решение(1)
комментарий/решение(1)
Задача №3. Внутри треугольника $ABC$ нашлась такая точка $P$, что $$\angle PBA=\angle PCB=\angle PCA=\angle PAC.$$ Докажите, что если $\angle B=60^\circ$, то $ABC$ — равносторонний.
(
Лим Э.,
Тнымкулов М.
)
комментарий/решение
комментарий/решение
Задача №4. В школе библиотекарь заявил: «В библиотеке есть сборник задач, в каждом разделе которого есть глава геометрии или комбинаторики.»
а) Бахыт утверждает, что во всех задачниках нет ни одной главы геометрии, а есть лишь одна глава комбинаторики. Следует ли из утверждения Бахыта, что библиотекарь соврал?
б) Эрик решил проверить слова библиотекаря. Он посмотрел четыре задачника, и суммарно нашёл десять разделов. Приметив главу геометрии, он пришёл к выводу, что библиотекарь ошибся. Сколько задачников в библиотеке этой школы? Какое наибольшее число глав комбинаторики мог посмотреть Эрик? (Считайте, что в одном разделе не более одной главы комбинаторики.)
комментарий/решение
а) Бахыт утверждает, что во всех задачниках нет ни одной главы геометрии, а есть лишь одна глава комбинаторики. Следует ли из утверждения Бахыта, что библиотекарь соврал?
б) Эрик решил проверить слова библиотекаря. Он посмотрел четыре задачника, и суммарно нашёл десять разделов. Приметив главу геометрии, он пришёл к выводу, что библиотекарь ошибся. Сколько задачников в библиотеке этой школы? Какое наибольшее число глав комбинаторики мог посмотреть Эрик? (Считайте, что в одном разделе не более одной главы комбинаторики.)
комментарий/решение
Задача №5. Даны целые числа от 2 до 26 (всего 25 чисел). Все эти числа нужно покрасить в цвета по следующему правилу: если какое-нибудь число является простым делителем какого-либо другого числа, то цвета этих чисел должны различаться. Какое наименьшее число цветов для этого необходимо использовать?
(
Камалеев А.
)
комментарий/решение(1)
комментарий/решение(1)
Задача №6. Для попарно различных действительных чисел $a,b,c$ выполнены равенства: $a^{2}(b+c)=b^{2}(a+c)=2025.$ Чему может равняться значение выражения $c^{2}(a+b)$?
(
Уалихан А.
)
комментарий/решение(1)
комментарий/решение(1)
Задача №7. Дана фигура Кенгуру, которая за раз ходит на 2 клетки по вертикали и на 2 клетки по горизонтали (то есть ходит из одного угла квадрата $3 \times 3$ в другую диагонально противоположную). Какое наибольшее число фигуры Кенгуру можно поставить на доску $6\times 6$ так, чтобы никакие две из них не били друг друга.
(
Тнымкулов М.
)
комментарий/решение
комментарий/решение
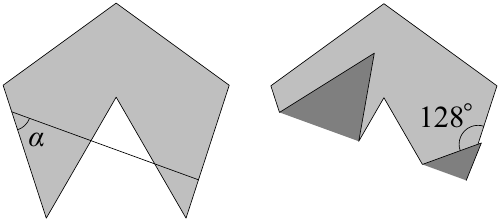
Задача №8. Из бумажного листа формы правильного пятиугольника вырезали правильный треугольник (две вершины треугольника совпадают с двумя вершинами пятиугольника). Затем под углом $\alpha$ провели прямую и согнули лист вдоль этой прямой, в результате чего образовался угол $128^\circ$. Найдите $\alpha$.
комментарий/решение(1)
комментарий/решение(1)