Городская Жаутыковская олимпиада по математике, 7 класс, 2025 год
Есеп №1. 1 сері мен 100 өтірікші бір қатарға тізіліп тұрып, кейін олар кезекшінің телефонын тығып қояды. Осыдан кейін әрқайсысы: «Телефон менің көршілерімнің бірінде» — деп айтты. Кезекші тек бір адамға ғана: «Телефонды сен алдың ба?» — деп сұрақ қойып, сол сұраққа алған жауап арқылы телефонның кімде екенін қателеспей анықтай ала ма? (Сері әрқашан шындықты, ал өтірікшілер тек өтірік айтады.)
комментарий/решение(1)
комментарий/решение(1)
Есеп №2. Он натурал санның қосындысы 2025-ке тең. Осы он санның ең үлкен ортақ бөлгішінің ең үлкен мәні неше тең бола алады?
комментарий/решение(1)
комментарий/решение(1)
Есеп №3. $ABC$ үшбұрышының ішінде $$\angle PBA = \angle PCB = \angle PCA = \angle PAC$$ болатындай $P$ нүктесі табылған. Егер $\angle B = 60^\circ$ болса, онда $ABC$ үшбұрышы теңқабырғалы екенін дәлелдеңіз.
(
Лим Э.,
Тнымкулов М.
)
комментарий/решение
комментарий/решение
Есеп №4. Мектеп кітапханашысы былай деді: «Кітапханада әр бөлімінде геометрия немесе комбинаторика тарауы бар есептер жинағы бар.»
а) Бахыт барлық есептер жинағында геометрия тарауы мүлдем жоқ, ал тек бір ғана комбинаторика тарауы бар деп мәлімдейді. Бахыттың бұл мәлімдемесінен кітапханашы өтірік айтты деп қорытынды жасауға бола ма?
б) Эрик кітапханашының сөзін тексермек болады. Ол 4 есептер жинағын қарап шығып, оларда барлығы 10 бөлім табады. Бір геометрия тарауын көріп, кітапханашы қателесті деген шешімге келеді. Бұл мектеп кітапханасында неше есептер жинағы бар? Эрик ең көбі неше комбинаторика тарауын көре алған? (Әр бөлімде бір ғана комбинаторика тарауы болуы мүмкін деп есептеңіз.)
комментарий/решение
а) Бахыт барлық есептер жинағында геометрия тарауы мүлдем жоқ, ал тек бір ғана комбинаторика тарауы бар деп мәлімдейді. Бахыттың бұл мәлімдемесінен кітапханашы өтірік айтты деп қорытынды жасауға бола ма?
б) Эрик кітапханашының сөзін тексермек болады. Ол 4 есептер жинағын қарап шығып, оларда барлығы 10 бөлім табады. Бір геометрия тарауын көріп, кітапханашы қателесті деген шешімге келеді. Бұл мектеп кітапханасында неше есептер жинағы бар? Эрик ең көбі неше комбинаторика тарауын көре алған? (Әр бөлімде бір ғана комбинаторика тарауы болуы мүмкін деп есептеңіз.)
комментарий/решение
Есеп №5. $2$-ден $26$-ға дейінгі бүтін сандар берілген (барлығы $25$ сан). Осы сандарды келесі шарт бойынша түрлі түстерге бояу қажет: егер бір сан екіншісінің жай көбейткіші болса, онда бұл екі сан түрлі түске боялуы тиіс. Осылай бояу жасау үшін кемінде неше түрлі түс қажет?
(
Камалеев А.
)
комментарий/решение(1)
комментарий/решение(1)
Есеп №6. Ешқандай екеуі тең емес $a,b,c$ сандары үшін $a^{2}(b+c)=b^{2}(a+c)=2025$ теңдіктері орындалады. $c^{2}(a+b)$ өрнегінің мәні нешеге тең бола алады?
(
Уалихан А.
)
комментарий/решение(1)
комментарий/решение(1)
Есеп №7. Бір уақытта 2 ұяшыққа тігінен және 2 ұяшықты көлденеңінен жылжытатын Кенгуру фигурасы берілген (яғни ол $3 \times 3$ шаршының бір бұрышынан диагональ бойынша қарама-қарсы ұяшыққа жылжиды). Ешқандай екеуі бір-бірін ұрмайтындай етіп $6\times 6$ өлшемді тақтаға ең көп дегенде неше кенгуру фигурасын орналастыруға болады?
(
Тнымкулов М.
)
комментарий/решение
комментарий/решение
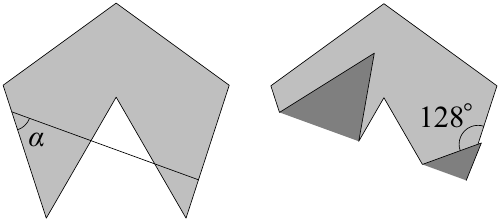
Есеп №8. Қағаздан жасалған дұрыс бесбұрыштан дұрыс үшбұрыш қиып алынды (үшбұрыштың екі төбесі бесбұрыштың екі төбесімен сәйкес келеді). Кейін қағазды $\alpha$ бұрышымен көлбеу түзу бойымен бүгіп, бүгілу нәтижесінде $128^\circ$ бұрышы пайда болды. $\alpha$ бұрышын табыңыз.
комментарий/решение(1)
комментарий/решение(1)