Городская Жаутыковская олимпиада по математике, 6 класс, 2025 год

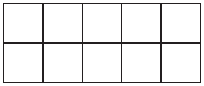
Есеп №1. $0$-ден $9$-ға дейінгі барлық бүтін сандарды $2 \times 5$ өлшемді кестенің ұяшықтарына, екінші бағаннан бастап әрбір келесі бағандағы сандардың қосындысы алдыңғысынан $1$-ге артық болатындай, бір реттен жазып шығыңыз. (Кестеде барлығы 5 баған бар, олардың есебі солдан оңға қарай жүргізіледі.)

( Дуйсенгали Н. )
комментарий/решение

Есеп №2. Вера мен Әділжан бір көшенің екі шетінде тұрады. Олардың үйлерінің арасында мектеп пен саябақ орналасқан, және бұл екі нысан жолды үш бірдей бөлікке бөледі. Бір күні Вера мен Әділжан үйлерінен бір уақытта жаяу шығып, бір-біріне қарама-қарсы беттеп жүріп, олар саябақтың жанында кездесті. Басқа күні Вера қайтадан Әділжанға қарсы шықты, бірақ бұл жолы ол велосипедпен шықты. Сонда оның жылдамдығы өзінің жаяу жүріс жылдамдығынан минутына $150$ метрге артық болды. Бұл жолы олар мектептің жанында кездесті. Әділжанның қалыпты жаяу жүру жылдамдығы қандай?
комментарий/решение

Есеп №3. Демалыс кезінде Эрикке бірнеше есептерден тұратын жинақ берілді. Бірінші күні ол барлық есептердің $10\%$-ын және қосымша тағы 6 есеп шығарды. Екінші күні ол қалған есептердің $10\%$-ын және тағы 10 есеп шығарды. Қалған есептерді ол үшінші күні бітірді. Есептер жинағында кемінде неше есеп болуы мүмкін?
комментарий/решение

Есеп №4. Шеңбер бойына $n$ бүтін сан жазылған. Әрбір сан өзінен кейінгі (сағат тілі бағытымен қарағанда) екі санның айырмасының модуліне тең. Егер барлық сандардың қосындысы $404$-ке тең болса, $n$-нің мүмкін болатын барлық мәндерін табыңыз.
комментарий/решение

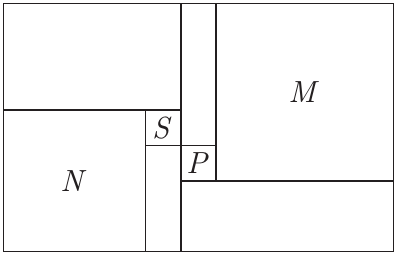
Есеп №5. Периметрі 2024-ке тең торлы тіктөртбұрыш берілген. Оны тор сызықтарының бойымен 4 тіктөртбұрышқа және 4 шаршыға бөлген (суретте олар $M$, $N$, $S$ және $P$ деп белгіленген). $S$ және $P$ шаршылары — өлшемі $1 \times 1$ болатын бірлік шаршылар екені белгілі. Бастапқы тіктөртбұрыштың қабырғаларын табыңыз. (Жауапты негіздеуді ұмытпаңыз.)

комментарий/решение

Есеп №6. 10 қағаз бөліктері бар. Бір операцияда Дайне бірнеше бөлікті таңдап, әрқайсысын 3 немесе 7 кішірек бөлікке бөле алады. Дайне бірнеше операцияда дәл 2025 қағаз бөлігін ала алады ма?
комментарий/решение

Есеп №7. Бір уақытта 2 ұяшыққа тігінен және 2 ұяшықты көлденеңінен жылжытатын Кенгуру фигурасы берілген (яғни ол $3 \times 3$ шаршының бір бұрышынан диагональ бойынша қарама-қарсы ұяшыққа жылжиды). Ешқандай екеуі бір-бірін ұрмайтындай етіп $6\times 6$ өлшемді тақтаға ең көп дегенде неше кенгуру фигурасын орналастыруға болады? ( Тнымкулов М. )
комментарий/решение

Есеп №8. Сыныпта қосымша үйірмелерге қатысатын 36 оқушы бар. Әр оқушы ең көп дегенде екі үйірмеге барады. Сонымен қатар, кез келген екі оқушы үшін олар баратын ортақ үйірме табылады. Қандай да бір үйірмеге кемінде 24 оқушы баратынын дәлелдеңіз.
комментарий/решение