Городская Жаутыковская олимпиада по математике, 6 класс, 2025 год

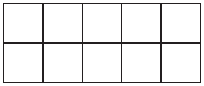
Задача №1. Расставьте все целые числа от 0 до 9 в клетки таблицы $2 \times 5$ по одному разу так, чтобы сумма чисел в каждом столбце, начиная со второго, была на 1 больше, чем в предыдущем. (В таблице всего 5 столбцов, и их счёт идёт слева направо.)

( Дуйсенгали Н. )
комментарий/решение

Задача №2. Вера и Адильжан живут на двух концах одной прямой дороги на улице. Между их домами расположены школа и парк так, что они делят эту дорогу на три равных участка. Однажды Вера и Адильжан одновременно вышли из своих домов и пошли пешком навстречу друг другу, и встретились возле парка. В другой день Вера снова вышла навстречу Адильжану, но уже на велосипеде, и двигалась на 150 метров в минуту быстрее. В этот раз они встретились возле школы. Какова обычная пешая скорость Адильжана?
комментарий/решение

Задача №3. На праздники Эрику дали набор задач. В первый день он решил $10 \%$ всех задач и ещё $6$ задач. Во второй день он решил $10 \%$ остатка, и после ещё $10$ задач. Оставшиеся задачи он решил в третий день. Какое наименьшее число задач могло быть в наборе?
комментарий/решение

Задача №4. На окружности записали $n$ целых чисел так, что каждое число равно модулю разности двух следующих чисел, стоящих по часовой стрелке. Найдите всевозможные значения $n$, если сумма всех чисел на окружности равна 404.
комментарий/решение

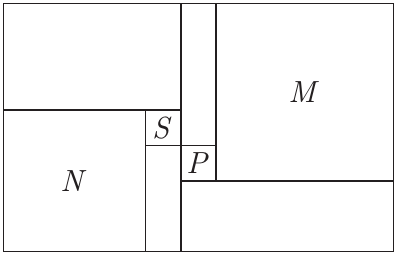
Задача №5. Дан клетчатый прямоугольник периметра 2024. Его по линиям сетки разбили на 4 прямоугольника и 4 квадрата (они обозначены через $N$, $S$, $P$ и $M$). Оказалось, что квадраты $S$ и $P$ — это квадраты размера $1\times1$. Найдите стороны исходного прямоугольника. (На забудьте обосновать свой ответ.)

комментарий/решение

Задача №6. Имеется $10$ кусков бумаги. За одну операцию Дайне может выбрать несколько кусков, и каждый разрезать на 3 или 7 меньших кусков. Сможет ли Дайне за несколько операции получить ровно 2025 куска бумаги?
комментарий/решение

Задача №7. Дана фигура Кенгуру, которая за раз ходит на 2 клетки по вертикали и на 2 клетки по горизонтали (то есть ходит из одного угла квадрата $3 \times 3$ в другую диагонально противоположную). Какое наибольшее число фигуры Кенгуру можно поставить на доску $6\times 6$ так, чтобы никакие две из них не били друг друга. ( Тнымкулов М. )
комментарий/решение

Задача №8. В классе учится 36 учеников, которые посещают дополнительные кружки. Каждый из них посещает не более двух кружков. Известно, что для любых двух учеников найдётся хотя бы один кружок, в который они оба записаны. Докажите, что существует кружок, в который записаны не менее 24 учеников.
комментарий/решение