Юниорская олимпиада по математике. Районный этап. 2022-2023 учебный год. 7 класс.
Задача №1. Даны стороны и высота параллелепипеда $a$, $b$, $c$ которые равны 5, 8 и 10. Найдите диагональ параллелепипеда.
A) $3\sqrt{21}$
B) $10\sqrt{3}$
C) $13$
D) $9\sqrt{19}$
E) $12\sqrt{2}$
комментарий/решение
A) $3\sqrt{21}$
B) $10\sqrt{3}$
C) $13$
D) $9\sqrt{19}$
E) $12\sqrt{2}$
комментарий/решение
Задача №2. Решите ребус: $C,BA+A,AA = B,A.$
A) $A=0$, $B=2$, $C=6$
B) $A=5$, $B=3$, $C=8$
C) $A=5$, $B=9$, $C=3$
D) $A=2$, $B=5$, $C=4$
E) $A=0$, $B=1$, $C=7$
комментарий/решение
A) $A=0$, $B=2$, $C=6$
B) $A=5$, $B=3$, $C=8$
C) $A=5$, $B=9$, $C=3$
D) $A=2$, $B=5$, $C=4$
E) $A=0$, $B=1$, $C=7$
комментарий/решение
Задача №3. Максат и Даулет решили подзаработать. Каждый из них решил положить по 30000 тенге в банк, а через год все деньги снять. Максат выбрал вклад «Уверенность»: за год сумма увеличивается на $20\%$, но при снятии банк взимает комиссию $10\%$. Даулет выбрал вклад «Надёжность»: за год сумма увеличивается на $40\%$, но при снятии банк взимает комиссию $20\%$. («Банк взимает комиссию $n\%$» означает то, что банк оставляет себе $n\%$ от текущей величины вклада, а оставшуюся часть вклада возвращает его владельцу.) Кто получит большую годовую прибыль от вклада? Чему будет равна разница? Если одинакова, то выберите 0.
A) Максат заработает на 2000 тенге больше/Мақсат 2000 теңгеге көбірек
B) Даулет заработает на 1500 тенге больше/Дәулет 1500 теңгеге көбірек
C) 0
D) Даулет заработает на 1200 тенге больше/Дәулет 1200 теңгеге көбірек
E) Максат заработает на 1000 тенге больше/Мақсат 1000 теңгеге көбірек
комментарий/решение
A) Максат заработает на 2000 тенге больше/Мақсат 2000 теңгеге көбірек
B) Даулет заработает на 1500 тенге больше/Дәулет 1500 теңгеге көбірек
C) 0
D) Даулет заработает на 1200 тенге больше/Дәулет 1200 теңгеге көбірек
E) Максат заработает на 1000 тенге больше/Мақсат 1000 теңгеге көбірек
комментарий/решение
Задача №4. Смешарики Крош, Ежик, Нюша и Бараш суммарно съели 86 конфет, причём каждый из них съел не менее 5 конфет. Известно, что: Нюша съела конфет больше, чем каждый из остальных смешариков; Крош и Ёжик суммарно съели 53 конфеты. Сколько конфет съела Нюша?
A) 35
B) 40
C) 28
D) 42
E) 33
комментарий/решение
A) 35
B) 40
C) 28
D) 42
E) 33
комментарий/решение
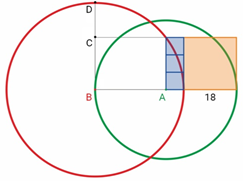
Задача №5. На рисунке ниже: три синие фигуры — квадраты; оранжевая фигура — квадрат со стороной 18; точка $A$ — центр зелёной окружности; точка $B$ — центр красной окружности. Найдите длину отрезка $CD$.
A) 10
B) 14
C) 18
D) 22
E) 12
комментарий/решение
A) 10
B) 14
C) 18
D) 22
E) 12
комментарий/решение
Задача №6. В магазине продаются орехи четырех видов: фундук, миндаль, кешью и фисташки. Серик хочет купить 1 килограмм орехов одного вида и ещё 1 килограмм орехов другого. Он вычислил, во сколько ему может обойтись такая покупка в зависимости от того, какие два вида орехов он выберет. Пять из шести возможных покупок Серик стоили бы 1900, 2070, 2110, 2330 и 2500 тенге. Сколько тенге составляет стоимость шестой возможной покупки?
A) 2300
B) 2290
C) 2500
D) 3000
E) 2000
комментарий/решение
A) 2300
B) 2290
C) 2500
D) 3000
E) 2000
комментарий/решение
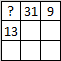
Задача №7. Магический квадрат — это таблица $3 \times 3$, в которой расставлены числа так, что суммы по всем строкам, столбцам и двум главным диагоналям одинаковы. На рисунке изображен магический квадрат, в котором все числа, кроме трёх, стёрты. Найдите, чему равно число в левом верхнем углу квадрата.
A) 14
B) 25
C) 92
D) 12
E) 90
комментарий/решение
A) 14
B) 25
C) 92
D) 12
E) 90
комментарий/решение
Задача №8. Все 25 учеников 7 «А» класса участвовали в викторине из трёх туров. В каждом туре каждый участник набрал некоторое количество очков. Известно, что в каждом туре, а также по сумме всех трех туров все участники набрали различное количество очков. Ученик 7 «А» Кайсар в первом туре викторины оказался третьим, во втором — четвертым, а в третьем — пятым. Какое самое низкое место мог занять Кайсар среди всех одноклассников по сумме очков за все три тура викторины?
A) 5
B) 8
C) 10
D) 15
E) 12
комментарий/решение
A) 5
B) 8
C) 10
D) 15
E) 12
комментарий/решение
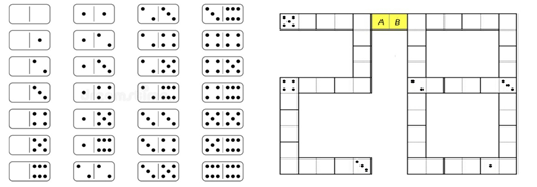
Задача №9. Набор из 28 различных доминошек выглядит так: Все эти 28 доминошек выложили так, что количество точек на соприкасающихся половинках доминошек одинаково. На некоторых половинках полностью стерли количество точек. В итоге получилась конструкция, изображенная на рисунке ниже (пустые половинки могли быть изначально пустыми, а могли содержать какое-то количество точек). Сколько точек на каждой из половинок жёлтой костяшки? Точек на половинке $A$: .... Точек на половинке $B$: ....
A) $A=2, B=4$
B) $A=5, B=6$
C) $A=8, B=2$
D) $A=5, B=2$
E) $A=2, B=5$
комментарий/решение
A) $A=2, B=4$
B) $A=5, B=6$
C) $A=8, B=2$
D) $A=5, B=2$
E) $A=2, B=5$
комментарий/решение
Задача №10. На стороне $BC$ прямоугольника $ABCD$ отмечена точка $K$. Точка $H$ на отрезке $AK$ такова, что $\angle AHD = 90^\circ$. Оказалось, что $AK = BC$. Сколько градусов составляет угол $ADH$, если $\angle CKD = 71^\circ$?
A) 60
B) 33
C) 45
D) 52
E) 55
комментарий/решение
A) 60
B) 33
C) 45
D) 52
E) 55
комментарий/решение
Задача №11. В остроугольном треугольнике $ABC$ проведена высота $BH$. Оказалось, что $CH = AB+AH$. Сколько градусов составляет угол $BAC$, если $\angle ABC=84^\circ$?
A) 64
B) 76
C) 53
D) 90
E) 45
комментарий/решение
A) 64
B) 76
C) 53
D) 90
E) 45
комментарий/решение
Задача №12. Простое число $p$ таково, что число $p+25$ является седьмой степенью простого числа. Чему может быть равно $p$? Укажите все возможные варианты.
A) 771
B) 299
C) 103
D) 527
E) 1307
комментарий/решение
A) 771
B) 299
C) 103
D) 527
E) 1307
комментарий/решение
Задача №13. Дан тупоугольный треугольник $ABC$ с тупым углом $C$. На его сторонах $AB$ и $BC$ отмечены точки $P$ и $Q$ соответственно так, что $\angle ACP = CPQ = 90^\circ$. Найдите длину отрезка $PQ$, если известно, что $AC = 25$, $CP = 20$, $\angle APC =\angle A+\angle B$.
A) 12
B) 16
C) 20
D) 42
E) 17
комментарий/решение
A) 12
B) 16
C) 20
D) 42
E) 17
комментарий/решение
Задача №14. Упростите выражение: $x^4+7x^3-21x^2-27x.$
A) $(x-1)(x-2)(x+7)x$
B) $(x+1)(x-3)(x+9)$
C) $(x+1)(x-3)(x+9)x$
D) $(x-1)(x+3)(x+9)x$
E) $(x+3)(x-1)(x+9)$
комментарий/решение
A) $(x-1)(x-2)(x+7)x$
B) $(x+1)(x-3)(x+9)$
C) $(x+1)(x-3)(x+9)x$
D) $(x-1)(x+3)(x+9)x$
E) $(x+3)(x-1)(x+9)$
комментарий/решение
Задача №15. Сумма трёх различных натуральных делителей нечётного натурального числа $n$ равна 10327. Какое наименьшее значение может принимать $n$?
A) 10327
B) 15633
C) 8725
D) 6735
E) 9817
комментарий/решение
A) 10327
B) 15633
C) 8725
D) 6735
E) 9817
комментарий/решение
Задача №16. На окружности $\omega$ по разные стороны от диаметра $AC$ расположены точки $B$ и $D$. Известно, что $AB = 3\sqrt{6}$, $CD = 3$, а площадь треугольника $ABC$ в три раза больше площади треугольника $BCD$. Найдите радиус окружности $\omega$.
A) 7
B) 9
C) 3,5
D) 5
E) 4,5
комментарий/решение
A) 7
B) 9
C) 3,5
D) 5
E) 4,5
комментарий/решение
Задача №17. Произведение положительных чисел $a$ и $b$ равно 1. Известно, что $(3a+2b)(3b+2a) = 295$. Найдите $a+b$.
A) 45
B) 12
C) 4
D) 7
E) 47
комментарий/решение
A) 45
B) 12
C) 4
D) 7
E) 47
комментарий/решение
Задача №18. В примере $(A - 5) : A+4 : B = 1$ с дробями некоторые двузначные натуральные числа заменили буквами $A$ и $B$. Какое наименьшее значение может принимать $A$? Какое наибольшее значение может принимать $B$?
A) $A=20, B= 80$
B) $A=15, B=76$
C) $A=1, B=15$
D) $A=3, B=101$
E) $A=27, B=123$
комментарий/решение
A) $A=20, B= 80$
B) $A=15, B=76$
C) $A=1, B=15$
D) $A=3, B=101$
E) $A=27, B=123$
комментарий/решение
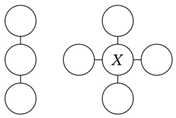
Задача №19. В кружочки на рисунке расставлены натуральные числа 13, 14, 15, 16, 17, 18, 19, 20 (каждое число в одном кружочке) так, что все три суммы трёх чисел вдоль каждой линии равны. Какое число может оказаться в кружочке $X$? Укажите все возможные варианты.
A) 15,18
B) 20, 25
C) Бесконечно много вариантов
D) Таких чисел не существует
E) 1
комментарий/решение
A) 15,18
B) 20, 25
C) Бесконечно много вариантов
D) Таких чисел не существует
E) 1
комментарий/решение
Задача №20. На стороне $AC$ равностороннего треугольника $ABC$ отмечена точка $D$. На отрезках $AD$ и $DC$ во внешнюю сторону от исходного треугольника построены равносторонние треугольники $ADE$ и $DCF$. Известно, что периметр треугольника $DEF$ равен 19, а периметр пятиугольника $ABCFE$ равен 43. Найдите длину отрезка $AB$ и $EF$.
A) 12, 5
B) 15, 12
C) 12, 7
D) 7, 15
E) 7, 12
комментарий/решение
A) 12, 5
B) 15, 12
C) 12, 7
D) 7, 15
E) 7, 12
комментарий/решение
Задача №21. Найдите все пары чисел $(x, y)$ таких, что: $x^2+3y = 7$, $x+y = 1$.
A) $(1, 2)$, $(4, 3)$
B) $(-1, 2)$, $(-3, 4)$
C) $(-1,-2)$, $(4,-3)$
D) $(-1, 2)$, $(4,-3)$
E) $(1, 2)$, $(4, 3)$
комментарий/решение
A) $(1, 2)$, $(4, 3)$
B) $(-1, 2)$, $(-3, 4)$
C) $(-1,-2)$, $(4,-3)$
D) $(-1, 2)$, $(4,-3)$
E) $(1, 2)$, $(4, 3)$
комментарий/решение
Задача №22. Решите уравнение: $1: (2-3: (4-5: (6-x)))= 7.$
A) 0
B) 1
C) $43:7$
D) 4
E) $121:31$
комментарий/решение
A) 0
B) 1
C) $43:7$
D) 4
E) $121:31$
комментарий/решение
Задача №23. В компании некоторые пары людей дружат (если $A$ дружит с $B$, то и $B$ дружит с $A$). Оказалось, что среди каждых 100 человек в компании количество пар дружащих людей нечетно. Найдите наибольшее возможное количество человек в такой компании.
A) 422
B) 263
C) 141
D) 101
E) 100
комментарий/решение
A) 422
B) 263
C) 141
D) 101
E) 100
комментарий/решение
Задача №24. Разложите на множители: $2x^4-2x^2-24.$
A) $(x-2)(x^2+3)(2x+4)$
B) $(x+2)(x+3)(2x-4)$
C) $(x-2)(x^4+3)(2x-4)$
D) $(x-3)(3x-2)(x^3+1)$
E) $(x+2)(x+3)(2x+4)$
комментарий/решение
A) $(x-2)(x^2+3)(2x+4)$
B) $(x+2)(x+3)(2x-4)$
C) $(x-2)(x^4+3)(2x-4)$
D) $(x-3)(3x-2)(x^3+1)$
E) $(x+2)(x+3)(2x+4)$
комментарий/решение
Задача №25. Представьте число 32 как произведение трёх целых множителей, сумма которых равна 3. Чему равен меньший из множителей?
A) 2
B) 4
C) 8
D) $-3$
E) $-4$
комментарий/решение
A) 2
B) 4
C) 8
D) $-3$
E) $-4$
комментарий/решение
Задача №26. В треугольнике $ABC$, $AB = BC = 29$ и $AC = 42$. Найдите площадь треугольника $ABC$.
A) 100
B) 420
C) 500
D) 609
E) 701
комментарий/решение
A) 100
B) 420
C) 500
D) 609
E) 701
комментарий/решение
Задача №27. Найдите последнюю цифру: $5^{23}+17^{17}+2^{2023}.$
A) 0
B) 1
C) 2
D) 3
E) 5
комментарий/решение
A) 0
B) 1
C) 2
D) 3
E) 5
комментарий/решение
Задача №28. Вычислите: $1+3+5+\ldots+2021+2023-2-4-6-\ldots-2020-2022.$
A) 1010
B) $-1010$
C) $-1012$
D) 1012
E) 1011
комментарий/решение
A) 1010
B) $-1010$
C) $-1012$
D) 1012
E) 1011
комментарий/решение
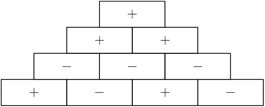
Задача №29. В пирамиде ячейка получает знак «+» если две ячейки под ним имеют одинаковый знак, а когда разные получает знак «-». На пирамиде снизу на рисунке есть 4 уровня. Сколькими разными способами можно расставить знаки на 4 ячейки снизу чтобы на вершине был знак «+»?
A) 2
B) 4
C) 8
D) 12
E) 16
комментарий/решение
A) 2
B) 4
C) 8
D) 12
E) 16
комментарий/решение
Задача №30. Сколько идеальных кубов между $2^8+1$ и $2^{18}+1$?
A) 4
B) 9
C) 10
D) 57
E) 58
комментарий/решение
A) 4
B) 9
C) 10
D) 57
E) 58
комментарий/решение