Юниорская олимпиада по математике. Районный этап. 2022-2023 учебный год. 7 класс.
Есеп №1. 5, 8 және 10 тең параллелепипедтің қабырғалары мен биіктігі берілген. Параллелепипедтің диагональін табыңыз.
A) $3\sqrt{21}$
B) $10\sqrt{3}$
C) $13$
D) $9\sqrt{19}$
E) $12\sqrt{2}$
комментарий/решение
A) $3\sqrt{21}$
B) $10\sqrt{3}$
C) $13$
D) $9\sqrt{19}$
E) $12\sqrt{2}$
комментарий/решение
Есеп №2. Ребусті шешіңіз: $C,BA+A,AA = B,A.$
A) $A=0$, $B=2$, $C=6$
B) $A=5$, $B=3$, $C=8$
C) $A=5$, $B=9$, $C=3$
D) $A=2$, $B=5$, $C=4$
E) $A=0$, $B=1$, $C=7$
комментарий/решение
A) $A=0$, $B=2$, $C=6$
B) $A=5$, $B=3$, $C=8$
C) $A=5$, $B=9$, $C=3$
D) $A=2$, $B=5$, $C=4$
E) $A=0$, $B=1$, $C=7$
комментарий/решение
Есеп №3. Мақсат пен Дәулет табыс тапқысы келіп, банкке отыз мың теңгеден салып, бір жылдан соң шешіп алатын болды. Мақсат «Сенімділік»-ті таңдады: Бір жыл ішінде салынған сомма жиырма пайызға көбейеді, бірақ ақшаны шешіп аларда Дәулет «Үміт»-ті таңдады: Бір жыл ішінде салынған сомма қырық пайызға көбейіп, комиссия 20 болады. Кім көбірек пайда көреді? Табыстарының айырмашылықтары қандай болады? Егерде табыстары бірдей болса 0 таңдаңыз.
A) Максат заработает на 2000 тенге больше/Мақсат 2000 теңгеге көбірек
B) Даулет заработает на 1500 тенге больше/Дәулет 1500 теңгеге көбірек
C) 0
D) Даулет заработает на 1200 тенге больше/Дәулет 1200 теңгеге көбірек
E) Максат заработает на 1000 тенге больше/Мақсат 1000 теңгеге көбірек
комментарий/решение
A) Максат заработает на 2000 тенге больше/Мақсат 2000 теңгеге көбірек
B) Даулет заработает на 1500 тенге больше/Дәулет 1500 теңгеге көбірек
C) 0
D) Даулет заработает на 1200 тенге больше/Дәулет 1200 теңгеге көбірек
E) Максат заработает на 1000 тенге больше/Мақсат 1000 теңгеге көбірек
комментарий/решение
Есеп №4. Крош, Ежик, Нюша және Бараш бірге 86 кәмпит жеді, әрқайсысы кемінде 5 кәмпит жеді. Нюша бәріненде көбірек кәмпит жеді. Крош пен Ежик бірге 53 кәмпит жеді. Нюша қанша кәмпит жеді?
A) 35
B) 40
C) 28
D) 42
E) 33
комментарий/решение
A) 35
B) 40
C) 28
D) 42
E) 33
комментарий/решение
Есеп №5. Төмендегі суретте: Үш көк фигура — шаршылар; Қызғылтсары фигура — қабырғасы 18 шаршы; $A$ нүктесі — жасыл шеңбердің центрі; $B$ нүктесі — қызыл шеңбердің центрі. $CD$ кесіндісінің ұзындығын табыңыз.
A) 10
B) 14
C) 18
D) 22
E) 12
комментарий/решение
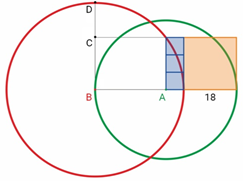
A) 10
B) 14
C) 18
D) 22
E) 12
комментарий/решение
Есеп №6. Дүкенде жаңғақтардың төрт түрі сатылады: фундук, миндаль, кешью және фисташкілер. Серік екі түрлі жаңғақтың әрқайсысынан 1 килограмм сатып алғысы келеді. Ол қандай жаңғақтарды таңдағанына қарай қанша ақша төлеуі мүмкін екенін есептеді. Алты түрлі бағаның бесеуі 1900, 2070, 2110, 2330 және 2500 болады. Алтыншының бағасын табыңыз.
A) 2300
B) 2290
C) 2500
D) 3000
E) 2000
комментарий/решение
A) 2300
B) 2290
C) 2500
D) 3000
E) 2000
комментарий/решение
Есеп №7. Сиқырлы $3 \times 3$ шаршы — бағандар, қатар мен екі диагональдағы сандардың қосындысы бір-біріне тең. Төменде сиқырлы шаршы бейнеленгенжәне үш саннан басқа сандарды өшіріп тастаған. Сұрақ белгісінің орнына сай келетін санды табыңыз.
A) 14
B) 25
C) 92
D) 12
E) 90
комментарий/решение
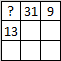
A) 14
B) 25
C) 92
D) 12
E) 90
комментарий/решение
Есеп №8. Үш кезеңнен тұратын викторинаға 7 «А» сыныбында оқитын барлық 25 бала қатысты. Әр кезеңде алған ұпайыжәне үш кезеңнің қосындысы әр балада әртүрлі екені белгілі. 7 «А» сыныбының оқушысы Қайсар бірінші кезеңде үшінші, екінші кезеңде өө төртінші, ал үшінші кезеңде өө бесінші болды.Қайсар үш кезеңнің қосындысы бойынша ең төмен қай орынды алуы мүмкін?
A) 5
B) 8
C) 10
D) 15
E) 12
комментарий/решение
A) 5
B) 8
C) 10
D) 15
E) 12
комментарий/решение
Есеп №9. 28 доминодан құралған жиынтық төмендегідей: Нүкте сандары бірдей доминоның жарты бөлігі бір-біріне тиіп тұратындай етіп 28 домино қойылды. Кейбір доминолардың жартысындағы нүктелерді түгелдей өшіріп тастады. Соңында төмендегідей фигура шықты (кейбір нүктелері жоқ доминоларда басынан бері нүкте болмауы мүмкін). $A$ бөлігіндегі нүктелер саны: $\ldots$. $B$ бөлігіндегі нүктелер саны: $\ldots$.
A) $A=2, B=4$
B) $A=5, B=6$
C) $A=8, B=2$
D) $A=5, B=2$
E) $A=2, B=5$
комментарий/решение
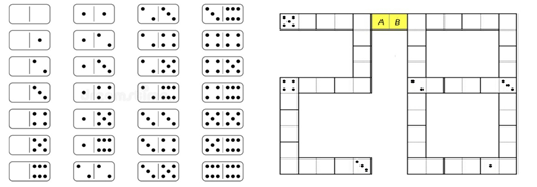
A) $A=2, B=4$
B) $A=5, B=6$
C) $A=8, B=2$
D) $A=5, B=2$
E) $A=2, B=5$
комментарий/решение
Есеп №10. $ABCD$ тіктөртбұрышының $BC$ қабырғасында $K$ нүктесі белгіленген. $\angle AHD = 90^\circ$ болатындай $AK$ кесіндісінде $H$ нүктесі белгіленген. $AK = BC$ екені белгілі болды. $\angle CKD = 71^\circ$ болса $ADH$ бұрышы нешеге тең болады?
A) 60
B) 33
C) 45
D) 52
E) 55
комментарий/решение
A) 60
B) 33
C) 45
D) 52
E) 55
комментарий/решение
Есеп №11. $ABC$ сүйір үшбұрышында $BH$ биіктігі жүргізілген. $CH = AB+AH$. $\angle ABC=84^\circ$ болса $BAC$ бұрышын табыңыз.
A) 64
B) 76
C) 53
D) 90
E) 45
комментарий/решение
A) 64
B) 76
C) 53
D) 90
E) 45
комментарий/решение
Есеп №12. $p+25$ жай санның жетінші дәрежесі болатындай жай сан $p$ таңдалған. $p$ қандай сандарға тең бола алады?
A) 771
B) 299
C) 103
D) 527
E) 1307
комментарий/решение
A) 771
B) 299
C) 103
D) 527
E) 1307
комментарий/решение
Есеп №13. Доғал үшбұрыш $ABC$-ның $C$ бұрышы доғал. $\angle ACP = CPQ = 90^\circ$ болатындай $AB$ және $BC$ қабырғаларында $P$ мен $Q$ нүктелері алынған. $AC = 25$, $CP = 20$, $\angle APC =\angle A+\angle B$ екені белгілі болса $PQ$ кесіндісі неге тең екенін табыңыз.
A) 12
B) 16
C) 20
D) 42
E) 17
комментарий/решение
A) 12
B) 16
C) 20
D) 42
E) 17
комментарий/решение
Есеп №14. Өрнекті ықшамдаңыз: $x^4+7x^3-21x^2-27x.$
A) $(x-1)(x-2)(x+7)x$
B) $(x+1)(x-3)(x+9)$
C) $(x+1)(x-3)(x+9)x$
D) $(x-1)(x+3)(x+9)x$
E) $(x+3)(x-1)(x+9)$
комментарий/решение
A) $(x-1)(x-2)(x+7)x$
B) $(x+1)(x-3)(x+9)$
C) $(x+1)(x-3)(x+9)x$
D) $(x-1)(x+3)(x+9)x$
E) $(x+3)(x-1)(x+9)$
комментарий/решение
Есеп №15. Натурал тақ $n$ санның үш әртүрлі натурал бөлгіштерінің қосындысы 10327 тең. Ең кіші $n$ мәні нешеге тең?
A) 10327
B) 15633
C) 8725
D) 6735
E) 9817
комментарий/решение
A) 10327
B) 15633
C) 8725
D) 6735
E) 9817
комментарий/решение
Есеп №16. $\omega$ шеңберінің $AC$ диаметрінің екі жағында $B$ және $D$ нүктелері орналасқан. $AB = 3\sqrt{6}$, $CD = 3$ екені белгілі, ал $ABC$ үшбұрышының ауданы $BCD$ үшбұрышының ауданынан үш есе үлкен. $\omega$ шеңберінің радиус табыңыз.
A) 7
B) 9
C) 3,5
D) 5
E) 4,5
комментарий/решение
A) 7
B) 9
C) 3,5
D) 5
E) 4,5
комментарий/решение
Есеп №17. $a$ және $b$ оң сандарының көбейтіндісі 1 тең. $(3a+2b)(3b+2a) = 295$ өрнек берілген болса $a+b$ нешеге тең?
A) 45
B) 12
C) 4
D) 7
E) 47
комментарий/решение
A) 45
B) 12
C) 4
D) 7
E) 47
комментарий/решение
Есеп №18. $(A - 5) : A+4 : B = 1$ теңдеуде кейбір екі таңбалы сандарды $A$ және $B$ сандарымен ауыстырған. $A$-ның мүмкін ең кіші мәні? $B$-ның мүмкін ең үлкен мәні?
A) $A=20, B= 80$
B) $A=15, B=76$
C) $A=1, B=15$
D) $A=3, B=101$
E) $A=27, B=123$
комментарий/решение
A) $A=20, B= 80$
B) $A=15, B=76$
C) $A=1, B=15$
D) $A=3, B=101$
E) $A=27, B=123$
комментарий/решение
Есеп №19. Дөңгелектерде қатар тұрған үш санның қосындысы тең болатындай етіп 13, 14, 15, 16, 17, 18, 19, 20 сандары қойылған. $X$-тің орнына қандай сан бола алады? Барлық жауаптарды көрсетіңіз.
A) 15,18
B) 20, 25
C) Бесконечно много вариантов
D) Таких чисел не существует
E) 1
комментарий/решение
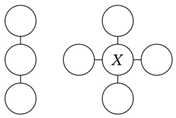
A) 15,18
B) 20, 25
C) Бесконечно много вариантов
D) Таких чисел не существует
E) 1
комментарий/решение
Есеп №20. Теңбұрышты үшбұрыш $ABC$-ның $AC$ қабырғасында $D$ нүктесі белгіленген. $AD$ және $DC$ кесінділерінде бастапқы үшбұрыштан сырттай $ADE$ мен $DCF$ теңбұрышты үшбұрыштар құралды. $DE$-тің периметрі 19-ға, ал $ABCFE$ бесбұрышының периметрі 43-ке тең. $AB$ мен $EF$ кесінділерінің ұзындықтарын табыңыз.
A) 12, 5
B) 15, 12
C) 12, 7
D) 7, 15
E) 7, 12
комментарий/решение
A) 12, 5
B) 15, 12
C) 12, 7
D) 7, 15
E) 7, 12
комментарий/решение
Есеп №21. $x^2+3y = 7$, $x+y = 1$ болатындай $(x, y)$ сандарының барлық жұптарын табыңыз.
A) $(1, 2)$, $(4, 3)$
B) $(-1, 2)$, $(-3, 4)$
C) $(-1,-2)$, $(4,-3)$
D) $(-1, 2)$, $(4,-3)$
E) $(1, 2)$, $(4, 3)$
комментарий/решение
A) $(1, 2)$, $(4, 3)$
B) $(-1, 2)$, $(-3, 4)$
C) $(-1,-2)$, $(4,-3)$
D) $(-1, 2)$, $(4,-3)$
E) $(1, 2)$, $(4, 3)$
комментарий/решение
Есеп №22. Теңдеуді шеш: $1: (2-3: (4-5: (6-x)))= 7.$
A) 0
B) 1
C) $43:7$
D) 4
E) $121:31$
комментарий/решение
A) 0
B) 1
C) $43:7$
D) 4
E) $121:31$
комментарий/решение
Есеп №23. Топта кейбір адамдар бір бірінен дос (егер $A$ $B$-мен дос болса, $B$ да $A$-мен дос). Әрбір 100 адамның ішінде бір-бірімен дос жұптардың саны тақекен. Осы топта мүмкін бола алатын ең үлкен адамдар санын табыңыз.
A) 422
B) 263
C) 141
D) 101
E) 100
комментарий/решение
A) 422
B) 263
C) 141
D) 101
E) 100
комментарий/решение
Есеп №24. Көбейткіштерге жіктеңіз: $2x^4-2x^2-24.$
A) $(x-2)(x^2+3)(2x+4)$
B) $(x+2)(x+3)(2x-4)$
C) $(x-2)(x^4+3)(2x-4)$
D) $(x-3)(3x-2)(x^3+1)$
E) $(x+2)(x+3)(2x+4)$
комментарий/решение
A) $(x-2)(x^2+3)(2x+4)$
B) $(x+2)(x+3)(2x-4)$
C) $(x-2)(x^4+3)(2x-4)$
D) $(x-3)(3x-2)(x^3+1)$
E) $(x+2)(x+3)(2x+4)$
комментарий/решение
Есеп №25. 32 санын соммасы 3-ке тең болатын бүтін үш көбейткіштің көбейтіндісі ретінде алыңыз. Көбейткіштердің ең кішісі неге тең?
A) 2
B) 4
C) 8
D) $-3$
E) $-4$
комментарий/решение
A) 2
B) 4
C) 8
D) $-3$
E) $-4$
комментарий/решение
Есеп №26. $ABC$ үшбырышында $AB = BC = 29$ және $AC = 42$. $ABC$ үшбырышының ауданын табыңыз.
A) 100
B) 420
C) 500
D) 609
E) 701
комментарий/решение
A) 100
B) 420
C) 500
D) 609
E) 701
комментарий/решение
Есеп №27. Төмендегі өрнекті соңғы цифрін табыңыз: $5^{23}+17^{17}+2^{2023}.$
A) 0
B) 1
C) 2
D) 3
E) 5
комментарий/решение
A) 0
B) 1
C) 2
D) 3
E) 5
комментарий/решение
Есеп №28. Есептеңіз: $1+3+5+\ldots+2021+2023-2-4-6-\ldots-2020-2022.$
A) 1010
B) $-1010$
C) $-1012$
D) 1012
E) 1011
комментарий/решение
A) 1010
B) $-1010$
C) $-1012$
D) 1012
E) 1011
комментарий/решение
Есеп №29. Пирамададағытекшенің ішінде «+» белгісі болу үшін сол текшенің астындағы екі текшеде бірдей белгі болуы тиіс, белгілер әртүрлі болған жағдайда «-» белгісі қойылады. Төмендегі пирамидада 4 деңгей бар. Ең үстінде «+» белгісі болатындай етіп қаншаәртүрлі тәсілмен астындағы төрт текшені толтыруға болады?
A) 2
B) 4
C) 8
D) 12
E) 16
комментарий/решение
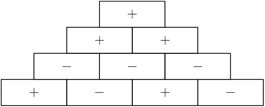
A) 2
B) 4
C) 8
D) 12
E) 16
комментарий/решение
Есеп №30. $2^8+1$ мен $2^{18}+1$ сандарының арасында қанша бүтін санның кубы бар?
A) 4
B) 9
C) 10
D) 57
E) 58
комментарий/решение
A) 4
B) 9
C) 10
D) 57
E) 58
комментарий/решение