5-я олимпиада им. Шалтая Смагулова, 7 класс, 2 тур

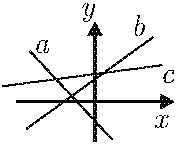
Задача №1.  Три прямые $a,b,c$ на рисунке ниже имеют угловые коэффициенты $A,B,C$ соответственно. Какое из чисел $A,B,C$ является:
   а) отрицательным;
   б) наибольшим;
   в) наименьшим?

комментарий/решение(1)

---

Задача №2.  Числа $a_1$, $a_2$, $\ldots$, $a_{20}$ это некая перестановка чисел $\frac11$, $\frac12$, $\ldots$, $\frac{1}{20}$. Оказалось, что для каждой из пар чисел $(a_1,a_2)$, $(a_3,a_4)$, $\ldots,$ $(a_{17},a_{18})$ выполнено свойство: модуль разности чисел в каждой паре равен их произведению, то есть $|a_1-a_2|=a_1a_2$, $|a_3-a_4|=a_3a_4,$ и т.д. Обязательно ли это свойство выполнено для пары $(a_{19},a_{20})$?
комментарий/решение(1)

---

Задача №3.  Сколько натуральных чисел, меньших 11111100111, записано только цифрами 0 и 1?
комментарий/решение(2)

---

Задача №4.  Произведение 25 натуральных чисел оканчивается на 25. Докажите, что среди них найдется 3 числа, произведение которых тоже оканчивается на 25.
комментарий/решение(1)

---

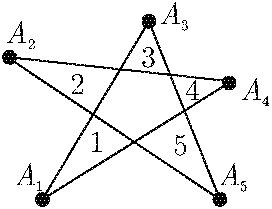
Задача №5.  Треугольник $ABC$, в котором $AB=AC$, будем называть равнобедренным треугольником при вершине $A$. Дана звезда, в которой отмечены треугольники с номерами 1, 2, 3, 4, 5, имеющие вершины $A_1,A_2,A_3,A_4,A_5$ соответственно. Могло ли оказаться так, что треугольники 1, 3, 5 являются равнобедренными при вершинах $A_1$, $A_3$, $A_5$ соответственно, а треугольники 2 и 4 также являются равнобедренными, но не при вершинах $A_2$, $A_4$ соответственно.

комментарий/решение

---