Городская Жаутыковская олимпиада по математике, 8 класс, 2023 год
Задача №1. Диагонали $AC$ и $BF$ правильного шестиугольника $ABCDEF$ пересекаются в точке $L$. Найдите отношение площади треугольника $ALB$ к площади шестиугольника.
комментарий/решение(1)
комментарий/решение(1)
Задача №2. Для любых положительных чисел $a,b,c$ докажите неравенство $$\frac{a}{{bc}} + \frac{b}{{ac}} + \frac{c}{{ab}} \ge \frac{2}{a} + \frac{2}{b} - \frac{2}{c}.$$ При каких положительных $a,b,c$ неравенство превращается в равенство?
комментарий/решение(2)
комментарий/решение(2)
Задача №3. Найдите все натуральные пары чисел $(x,y)$, для которых выполнено равенство $x^3=y^2+1$.
комментарий/решение(2)
комментарий/решение(2)
Задача №4. На рисунке дана карта из шестиугольников. На каждый шестиугольник можно поставить башню, защищающий сам шестиугольник на котором он стоит и шестиугольники вокруг неё. Какое наименьшее возможное количество башен необходимо, чтобы защитить все шестиугольники на карте? Считайте что башня, поставленная на рисунке поставлена только для наглядности, чтобы показать какие шестиугольники она защищает.
комментарий/решение(2)
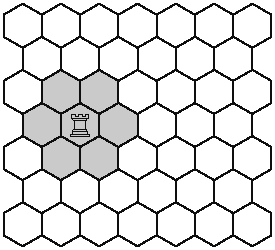
комментарий/решение(2)
Задача №5. Дан бильярдный стол размера $5 \times 7$, состоящий из квадратных клеток с четырьмя лузами в углах. Шар можно ставить в любой угол (т.е. вершину) любой клетки и ударить так, чтобы шар начал двигаться по прямой линии, которая образует со сторонами стола угол в $45^\circ$.
Углы, которые траектория шара образует со стенкой до и после соударения, равны;
скорость шара не меняется;
шар можно представить точкой, он попадает в лузу, только если его координаты точно совпадают с координатами какой-то лузы.
Из каких вершин клетки можно гарантировать, что при ударе можно попасть в лузу?
комментарий/решение
Углы, которые траектория шара образует со стенкой до и после соударения, равны;
скорость шара не меняется;
шар можно представить точкой, он попадает в лузу, только если его координаты точно совпадают с координатами какой-то лузы.
Из каких вершин клетки можно гарантировать, что при ударе можно попасть в лузу?
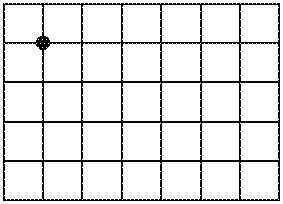
комментарий/решение
Задача №6. Школьник заметил, что месяц май 2023 года начинается с понедельника. Существует ли год, в котором ни один месяц не начинается с понедельника?
комментарий/решение
комментарий/решение
Задача №7. Для действительного числа $x$ выполнено равенство $x^2+x+1=0.$ Найдите значение выражения $x^{2023}+ \frac{1}{x^{2023}}$.
комментарий/решение(2)
комментарий/решение(2)
Задача №8. Высоты $BD$ и $CE$ остроугольного треугольника $ABC$ пересекаются в точке $H$. Пусть $\omega$ — описанная окружность треугольника $ABC$, а $M$ — середина стороны $BC$. Прямая $BD$ и луч $MH$ пересекают $\omega$ в точках $Y$ и $X$ соответственно. Касательная прямая к $\omega$ в точке $C$ пересекает прямую $DE$ в точке $Z$. Докажите, что точки $X$, $Y$, $Z$ лежат на одной прямой.
комментарий/решение(3)
комментарий/решение(3)