Городская Жаутыковская олимпиада по математике, 8 класс, 2023 год
Есеп №1. $ABCDEF$ дұрыс алтыбұрышының $AC$ және $BF$ диагональдары $L$ нүктесінде қиылысады. $ALB$ үшбұрышының ауданының алтыбұрыштың ауданына қатынасын табыңыз.
комментарий/решение(1)
комментарий/решение(1)
Есеп №2. Кез келген оң $a,b,c$ сандары үшін $$\frac{a}{{bc}} + \frac{b}{{ac}} + \frac{c}{{ab}} \ge \frac{2}{a} + \frac{2}{b} - \frac{2}{c}$$ теңсіздігін дәлелдеңіз. Қандай оң $a,b,c$ сандары үшін теңсіздік теңдікке айналады?
комментарий/решение(2)
комментарий/решение(2)
Есеп №3. $x^3=y^2+1$ теңдігі орындалатындай барлық $(x,y)$ натурал сандар жұптарын табыңыз.
комментарий/решение(2)
комментарий/решение(2)
Есеп №4. Суретте алтыбұрыштар картасы көрсетілген. Әрбір алтыбұрышқа ол тұрған алтыбұрышты және оның айналасындағы алтыбұрыштарды қорғайтын мұнара қоюға болады. Картадағы барлық алтыбұрыштарды қорғау үшін осы картаға ең аз дегенде неше мұнара қою керек? Суретте көрсетілген мұнараның ол қандай алтыбұрыштарды қорғайтынын көрсету үшін ғана мысал ретінде көрстілгенін ескеріңіз.
комментарий/решение(2)
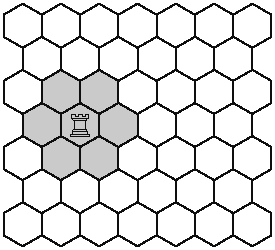
комментарий/решение(2)
Есеп №5. Бұрыштарында төрт қалтасы бар шаршы ұяшықтардан тұратын $5 \times 7$ бильярд үстелі берілген. Бильярд шарын кез келген ұяшықтың кез келген бұрышына (яғни төбесіне) қойып, сосын үстелдің бүйірлерімен $45^\circ$ бұрышын құрайтын түзу сызық бойымен қозғала бастайтындай етіп соғуға болады.
Шардың траекториясының соқтығысқа дейін және одан кейінгі қабырғамен жасайтын бұрыштары тең;
шардың жылдамдығы өзгермейді;
шарды нүкте ретінде қабылдауға болады, ал егер қозғалу барысында оның координаттары қандай да бір қалтаның координаттарымен дәл беттессе ғана, ол қалтаға кіреді.
Ұяшықтардың қай төбелерінен шарды ұрғанда ол қалтаға түседі деп кепілдік бере аласыз?
комментарий/решение
Шардың траекториясының соқтығысқа дейін және одан кейінгі қабырғамен жасайтын бұрыштары тең;
шардың жылдамдығы өзгермейді;
шарды нүкте ретінде қабылдауға болады, ал егер қозғалу барысында оның координаттары қандай да бір қалтаның координаттарымен дәл беттессе ғана, ол қалтаға кіреді.
Ұяшықтардың қай төбелерінен шарды ұрғанда ол қалтаға түседі деп кепілдік бере аласыз?
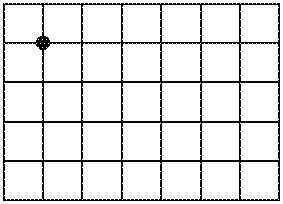
комментарий/решение
Есеп №6. Оқушы 2023 жылдың мамыр айы дүйсенбіден басталатынын байқады. Ешқандай айы дүйсенбіден басталмайтын жыл табылады ма?
комментарий/решение
комментарий/решение
Есеп №7. Нақты $x$ саны үшін $x^2+x+1=0$ теңдігі орындалады. $x^{2023}+ \frac{1}{x^{2023}}$ өрнегінің мәнін табыңыз.
комментарий/решение(2)
комментарий/решение(2)
Есеп №8. Сүйірбұрышты $ABC$ үшбұрышының $BD$ және $CE$ биіктіктері $H$ нүктесінде қиылысады. $\omega$ — $\triangle ABC$-ға сырттай сызылған шеңбер, ал $M$ — $BC$ қабырғасының ортасы. $BD$ түзуі мен $MH$ сәулесі $\omega$-ны, сәйкесінше, $Y$ және $X$ нүктелерінде қиыды. $\omega$-ға $C$ нүктесінде жүргізілген жанама түзу $DE$-ні $Z$ нүктеде қияды. $X$, $Y$, $Z$ нүктелері бір түзудің бойында жатқанын дәлелдеңіз.
комментарий/решение(3)
комментарий/решение(3)