қазақша
русский6-шы халықаралық Жәутіков олимпиадасы, 2010 жыл
Полные решения этих задач опубликованы в книге, доступный для заказа по ссылке
Есеп №1. ${{p}^{3}}-{{q}^{7}}=p-q$ теңдеуін қанағаттандыратын барлық $p$ және $q$ жай сандарын тап.
комментарий/решение(3)
комментарий/решение(3)
Есеп №2. Шеңберге іштей сызылған $ABCD$ төртбұрышында $AB=AD$ екені белгілі. $BC$ және $CD$ қабырғалаларынан $MN=BM+DN$ болатындай етіп сәйкесінше $M$ және $N$ нүктелері алынған. $AM$ және $AN$ түзулері $ABCD$ төртбұрышына сырттай сызылған шеңберді екінші рет сәйкесінше $P$ және $Q$ нүктелерінде қияды. $APQ$ үшбұрышының биіктіктерінің қиылысу нүктесі $MN$ кесіндісіне тиісті екенін дәлелде.
комментарий/решение(1)
комментарий/решение(1)
Есеп №3. Торкөз қағаздың түзу сызықтарымен шектеліп алынған тіктөртбұрыш фигуралардың мынадай үш түріне бөлшектенген: табаны екі торкөздің қабырғасынан тұратын теңқабырғалы тік бұрышты үшбұрыштар -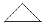 
, бір торкөзден тұратын шаршылар - 
, торкөздердің екі қабырғасынан және екі диагоналдарымен шектелген параллелограмдар -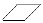 
(көрсетілген фигуралар бұрылып, немесе төңкеріліп тұруы мүмкін). Бөлшектеуден пайда болған үшінші түрдегі фигуралардың саны жұп болатыны дәлелде.
комментарий/решение(2)
, бір торкөзден тұратын шаршылар -
, торкөздердің екі қабырғасынан және екі диагоналдарымен шектелген параллелограмдар - (көрсетілген фигуралар бұрылып, немесе төңкеріліп тұруы мүмкін). Бөлшектеуден пайда болған үшінші түрдегі фигуралардың саны жұп болатыны дәлелде.
комментарий/решение(2)
Есеп №4. Тақтаға $1,2, \ldots,n$ натурал сандары жазылған, $n > 2$. Әр минутта тақтадан екі сан өшіріліп, орынына олардың қосындысының ең кіші жай бөлгіші жазылады. Ең соңында тақтада 97 саны қалды. Қандай ең кіші $n$ үшін осылай болуы мүмкін?
комментарий/решение(1)
комментарий/решение(1)
Есеп №5. Дұрыс $n$-бұрыштың әрбір төбесінде бір дойбы тасы орналасқан. Бір жүрісте кез келген көрші екі дойбы тасының орындарын ауыстыруға болады. Әрбір дойбы тасын бастапқыда тұрған төбесінен сағат тілімен $\left[ \dfrac{n}{2} \right]$ позицияға жылжытып алынған орналастыруды алу үшін ең кемі қанша жүріс қажет?
комментарий/решение
комментарий/решение
Есеп №6. Сүйірбұрышты $ABC$ үшбұрышының қабырғаларының ұзындықтары әртүрлі. $O,I,H$ арқылы сәкесінше $ABC$ үшбұрышының сырттай сызылған шеңберінің центрін, іштей сызылған шеңберінің центрін және биіктіктерінің қиылысу нүктелерін белгілейік. Дәлелдеңдер:
a) $\angle OIH > {{90}^{\circ }}$;
b) $\angle OIH > {{135}^{\circ }}$.
комментарий/решение(2)
a) $\angle OIH > {{90}^{\circ }}$;
b) $\angle OIH > {{135}^{\circ }}$.
комментарий/решение(2)