Математикадан республикалық олимпиада, 2015-2016 оқу жылы, 11 сынып
Есеп №1. Кел келген натурал сан үшін, келесі тұжырымды дәлелдеңіздер: осы санның барлық натурал бөлгіштерін, кез келген екі көрші тұрған бөлгіштердің біреуі екіншісіне бөлінетіндей, шеңбер бойымен қойып шығуға болады.
(
Д. Елиусизов
)
комментарий/решение(1)
комментарий/решение(1)
Есеп №2. Келесі шартты қанағаттандыратын барлық рационал $a$ сандарын табыңыздар: $\left[ {{x}^{a}} \right]\cdot \left\{ {{x}^{a}} \right\}=q$ теңдеуінің рационал $x$ шешуі болмайтындай, шексіз көп оң рационал $q$ саны бар.
(
А. Васильев
)
комментарий/решение(2)
комментарий/решение(2)
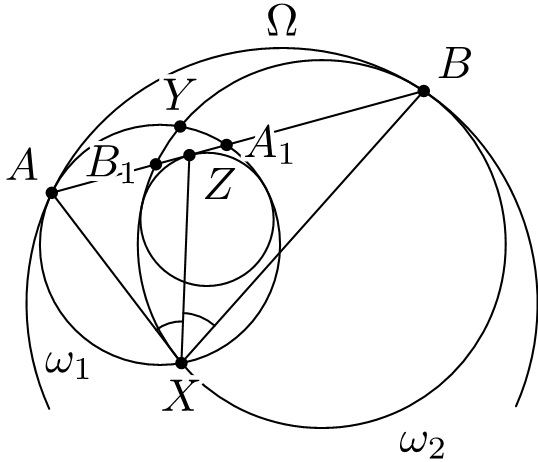
Есеп №3. $X$ және $Y$ нүктелерінде қиылысатын $\omega_1$ және $\omega_2$ шеңберлері $\Omega$ шеңберінің ішінде орналасқан, және оны $A$ және $B$ нүктелерінде жанайды. $AB$ түзуі екінші рет $\omega_1$ және $\omega_2$ шеңберлерін сәйкесінше $A_1$ және $B_1$ нүктерелінде қисын. $A_1B_1X$ қисықсызықты үшбұрышына іштей сызылған шеңбер $A_1B_1$ қабырғасын $Z$ нүктесінде жанасын. $\angle AXZ = \angle BXZ$ теңдігін көрсетіңіз.
комментарий/решение(2)
комментарий/решение(2)
Есеп №4. Теңбүйірлі $ABC$ үшбұрышында $H$ нүктесі — $AB$ табанының ортасы, ал $M$ — $BH$ кесіндісінің ортасы. $HK$ — $ACH$ үшбұрышының биіктігі, ал $CM$ және $BK$ түзулері $L$ нүктесінде қиылысады. $BC$ түзуіне $B$ нүктесінде жүргізілген перпендикуляр мен $LH$ түзуі $N$ нүктесінде қиылысады. $BCN$ бұрышының өлшемі $ACB$ бұрышының өлшемінен екі есе кіші екенін дәлелдеңіз.
(
М. Кунгожин
)
комментарий/решение(2)
комментарий/решение(2)
Есеп №5. Жазықтықта 101 көк және 101 қызыл нүктелер таңдалған, және кез келген үш нүкте бір түзудің бойында жатпайды. Екі ұшы да қызыл болатын барлық кесінділер ұзындықтарының қосындылары 1-ге тең (яғни $101\cdot 100/2$ кесінділер қосындысы), екі ұшы да көк болатын барлық кесінділер ұзындықтарының қосындылары да 1-ге тең, ал ұштары әр түсті болатын кесінділер ұзындықтарының қосындысы 400-ге тең. Барлық қызыл нүктелер түзудің бір жағында, ал барлық көк нүктелер сол түзудің басқа жағында болатындай түзу жүргізуге болатынын дәлелдеңіз.
(
Ким А.
)
комментарий/решение(1)
комментарий/решение(1)
Есеп №6. Оң сандардан тұратын, қатаң өспелі және шексіз $\{{{a}_{n}}\}$ тізбегі кез келген натурал $n$ үшін келесі шартты қанағаттандырады:
\[{{a}_{n+2}}={{({{a}_{n+1}}-{{a}_{n}})}^{\sqrt{n}}}+{{n}^{-\sqrt{n}}}.\]
Кез келген $C > 0$ үшін, ${{a}_{m(C)}} > C$ шарты орындалатын $C$-ға тәуелді $m(C)$ саны табылатынын дәлелдеңіз.
(
Сатылханов К.
)
комментарий/решение(1)
комментарий/решение(1)