8-я олимпиада им. Шалтая Смагулова, 7 класс, 1 тур

Есеп №1. Орманның $\frac{1}{4}$ бөлігіндегі ағаштың $40\%$-ы, ал қалған бөлігіндегі ағаштың $20\%$-ы кесілген. Ормандағы барлық ағаштың неше пайызы кесілген?
комментарий/решение

Есеп №2. $ABC$ үшбұрышында $AK$ және $BL$ биссектрисалары $O$ нүктесінде қиылысады. $AOB$ бұрышы $ALB$ бұрышынан 25 градусқа, ал $AKB$ бұрышынан 45 градусқа артық. $ACB$ бұрышы неше градусқа тең?
комментарий/решение

Есеп №3. Есептеңіз: $(4^8:8^4):(2^8:8^2):(2^4:4^2).$
комментарий/решение

Есеп №4. Оқушы келесі шарттарды қанағаттандыратын барлық натурал сандарды жазды: әр жазылған сан 2025-тен артық саннан кіші және әр жазылған сан 1952-ден кіші саннан артық. Оқушы неше сан жазды?
комментарий/решение

Есеп №5. Цифрларының қосындысы, бірінші цифрсыз 20-ға, екінші цифрсыз 14-ке, үшінші цифрсыз 17-ге, төртінші цифрсыз 12-ге тең болатын төрт таңбалы санды табыңыз.
комментарий/решение(1)

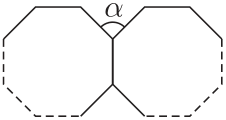
Есеп №6. Екі бірдей дұрыс $n$-бұрышты қабырғаларымен біріктіру арқылы $\alpha=40^\circ$ бұрышын алған (суретті қараңыз). $n$ санын табыңыз.

комментарий/решение

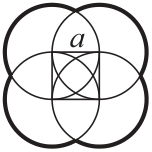
Есеп №7. Суретте төрт шеңбердің центрлері қабырғасы $a=10$ болатын шаршының төбелерінде жатыр. Жуан сызықпен сызылған қисықсызықты фигураның ұзындығын табыңыз. (Бұл есепте $\pi=3$ деп алыңыз.)

комментарий/решение

Есеп №8. Егер натурал $n$ санының алдына 1 цифрын қосып жазсақ, онда сол сан 9 есе өседі. Осындай барлық $n$ сандарының ішінде ең кішісі нешеге тең?
комментарий/решение

Есеп №9. Натурал жұп $n$ санының барлық бөлгіштерін бір қатарға өсу ретімен жазған. Сол жақтан бастап есептегенде екінші тұрған сан оң жақтан бастап есептегендегі екінші саннан 615-ке кем екені белгілі. $n$ санын табыңыз.
комментарий/решение

Есеп №10. Асан біртүрлі олимпиадаға қатысты. Оған берілген 20 есептің әр 10 оңай есептің дұрыс жауабына ол 2 ұпай, ал әр 10 қиын есептің дұрыс жауабына 3 ұпай алады. Бірақ ол қате жауап берсе, әр жеңіл есеп үшін 3 ұпай, ал әр қиын есеп үшін 2 ұпай шегеріледі. Өзіне сенімді Асан барлық есептерге жауап беріп, 20 ұпай алды. Ол неше есепке дұрыс жауап берді?
комментарий/решение

Есеп №11. Суретте 1-ден 16-ға дейінгі натурал сандармен толтырылған $4\times 4$ өлшемді сиқырлы шаршы көрсетілген. Шаршыда сол жоғарғы ұяшықта 16 саны тұр. Жұлдызшамен белгіленген ұяшықтардағы сандардың қосындысын табыңыз. (Сиқырлы шаршы деп – әр жолдағы, әр бағандағы және екі басты диагональдағы сандардың қосындысы бірдей болатын шаршыны айтамыз.)

комментарий/решение

Есеп №12. Өзін және 1-ді қоса есептегенде дәл 12 әртүрлі бөлгіші бар ең кіші натурал санды табыңыз.
комментарий/решение

Есеп №13. Сыныптағы ұлдардың пайыздық үлесі 94$\%$-дан артық. Бұл сыныпта кем дегенде қанша оқушы болуы мүмкін? (Сыныпта кем дегенде бір қыз бар.)
комментарий/решение(1)

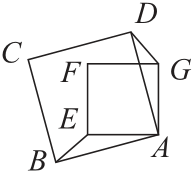
Есеп №14. Суретте $ABCD$ шаршысының периметрі 60-қа, $AEFG$ шаршысының периметрі 40-қа, $ABE$ үшбұрышының периметрі 31-ге тең. $DG$ кесіндісінің ұзындығын табыңыз.

комментарий/решение

Есеп №15. Текше берілген. Төбелері осы текшенің төбелерінде жататын неше теңқабырғалы үшбұрыш бар?
комментарий/решение

Есеп №16. Қабырғасы 24-ке болатын теңқабырғалы $ABC$ үшбұрышы берілген. Түзу $AB$, $BC$ кесінділерін және $AC$-ның созындысын, сәйкесінше, $D$, $E$ және $F$ нүктелерінде қияды ($C$ нүктесі $AF$ кесіндісінде жатыр). Егер $BD = CE = CF$ болса, $BD$ кесіндісінің ұзындығын табыңыз.
комментарий/решение

Есеп №17. Теңсіздіктер жүйесінің екі ең үлкен бүтін шешімдерінің көбейтіндісін табыңыз: $x^3\le 729 \le x^2$.
комментарий/решение

Есеп №18. Теңдіктен натурал $n$ санын табыңыз: $1+2+\ldots+(n-1)+n+(n-1)+\ldots+2+1=676.$
комментарий/решение(1)

Есеп №19. $A=\frac{4}{1\cdot 3}-\frac{8}{3\cdot 5}+\frac{12}{5\cdot 7}-\frac{16}{7\cdot 9}+\frac{20}{9\cdot 11}-\ldots-\frac{2024}{1011\cdot 1013}$ болсын. $1013\cdot A$ өрнегінің мәнін табыңыз.
комментарий/решение(1)

Есеп №20. Арман $1\cdot 7\cdot 13\cdot 19\cdot 25\cdot \ldots\cdot 2023$ көбейтіндісін $5^x \cdot 7^y \cdot z$ түріне келтіріп жазды, мұнда $x$, $y$, $z$ — натурал сандар және $z$ саны 5-ке де, 7-ге бөлінбейтін сан. $x+y$ қосындысының мәнін табыңыз.
комментарий/решение