Европейская математическая олимпиада среди девочек (EGMO). 2023 год. Словения
Есеп №1. $a_1, a_2, \ldots, a_n$ нақты оң сандары берілген, мұнда $n \geqslant 3$. Әрбір $1 \leqslant i \leqslant n$ үшін $b_i = \frac{a_{i-1} + a_{i+1}}{a_i}$ деп алайық (мұнда $a_0 = a_n$, ал $a_{n+1} = a_1$ деп есептейміз). Барлық $1 \leqslant i, j \leqslant n$ үшін $a_i \leqslant a_j$ болса және тек қана сол кезде $b_i \leqslant b_j$ орындалатыны белгілі. $a_1 = a_2 = \cdots = a_n$ екенін дәлелдеңіз.
комментарий/решение(2)
комментарий/решение(2)
Есеп №2. Сүйірбұрышты $ABC$ үшбұрышы берілген. $AD$ — үшбұрышқа сырттай сызылған шеңбер диаметрі. $K$ және $L$ нүктелері, сәйкесінше, $AB$ және $AC$ кесінділерінде жатқан нүктелер, мұнда $DK$ және $DL$ — $AKL$ үшбұрышына сырттай сызылған шеңберді жанайтын түзулер. $KL$ түзуі $ABC$ үшбұрышының ортоцентрі арқылы өтетінін дәлелдеңіз.
Үшбұрыштың ортоцентрі — оның биіктіктерінің қиылысу нүктесі.
комментарий/решение(1)
Үшбұрыштың ортоцентрі — оның биіктіктерінің қиылысу нүктесі.
комментарий/решение(1)
Есеп №3. $k$ — оң бүтін сан болсын. Лексида тек $A$ және $B$ әріптерінен тұратын $k$ әріптік бірнеше сөзден құралған $\mathcal{D}$ сөздігі бар. Ол әрбір бағанда жоғарыдан төмен қарай оқығанда және әрбір жолда солдан оңға қарай оқығанда $\mathcal{D}$-дегі сөз алынатындай $k \times k$ өлшемді кестенің әр ұяшығына $A$ не $B$ әрпін жазғысы келеді.
$m$ санының қандай ең кіші бүтін мәнінде $\mathcal{D}$-да кемінде $m$ әртүрлі сөз болады, әрі $\mathcal{D}$-да қандай сөздер болмаса да, Лекси кепілді түрде жоғарыдағы шарттар орындалатындай берілген тақтаны толтыра алады?
комментарий/решение
$m$ санының қандай ең кіші бүтін мәнінде $\mathcal{D}$-да кемінде $m$ әртүрлі сөз болады, әрі $\mathcal{D}$-да қандай сөздер болмаса да, Лекси кепілді түрде жоғарыдағы шарттар орындалатындай берілген тақтаны толтыра алады?
комментарий/решение
Есеп №4. Турбо ұлуы ұзындығы 1-ге тең шеңбердің бір нүктесінде орналасқан. $c_1, c_2, c_3, \ldots$ — оң нақты сандардан құралған шексіз тізбек берілген. Турбо осы сандардың әрқайсысына сәйкес шеңбер бойымен сағат тілінің бағытымен немесе кері бағытта жылжи алады.
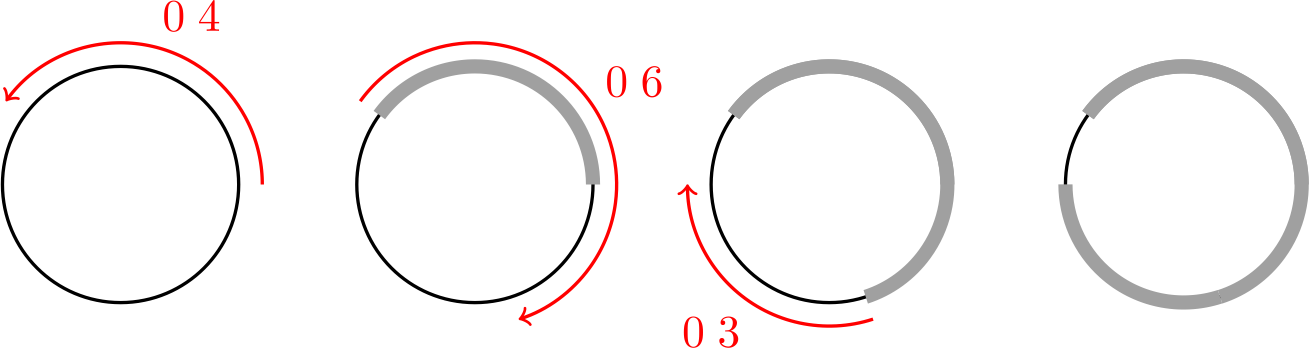
Мысалы, егер $c_1, c_2, c_3, \ldots = 0.4, 0.6, 0.3, \ldots$ болса, Турбо мынадай қозғалысты таңдай алады:
Келесі қасиетті қанағаттандыратын ең үлкен тұрақты $C > 0$ санын табыңыз: кез келген оң нақты $c_1, c_2, c_3, \ldots$ сандары үшін $c_i < C$ орындалады, әрі Турбо осы тізбекті зерттегеннен кейін, шеңбердегі қандай да бір нүкте тауып, сол нүктеге ешқашан келмейтіндей (және аттап өтпейтіндей) нүкте тауып ала алады.
комментарий/решение
Мысалы, егер $c_1, c_2, c_3, \ldots = 0.4, 0.6, 0.3, \ldots$ болса, Турбо мынадай қозғалысты таңдай алады:
Келесі қасиетті қанағаттандыратын ең үлкен тұрақты $C > 0$ санын табыңыз: кез келген оң нақты $c_1, c_2, c_3, \ldots$ сандары үшін $c_i < C$ орындалады, әрі Турбо осы тізбекті зерттегеннен кейін, шеңбердегі қандай да бір нүкте тауып, сол нүктеге ешқашан келмейтіндей (және аттап өтпейтіндей) нүкте тауып ала алады.
комментарий/решение
Есеп №5. $s \geqslant 2$ — бүтін оң сан. Әрбір бүтін оң сан $k$ үшін оның кері $k'$ мәнін анықтаймыз: $k = as + b$ түрінде жазып, мұндағы $a, b$ — теріс емес бүтін сандар және $b < s$, содан кейін $k' = bs + a$ деп қоямыз. $n$ — оң бүтін сан болсын, және $d_1 = n$, ал $d_{i+1}$ — $d_i$ санының кері мәні болатын $d_1, d_2, \ldots$ тізбегін құрайық.
Егер бұл тізбекте 1 саны кездессе, онда $n$ санын $s^2-1$ санына бөлгенде қалдық 1-ге немесе $s$-ке тең екенін дәлелдеңіз, және оған кері қасиетті дәлелдеңіз: егер $n$ санын $s^2-1$ санына бөлгенде қалдық 1-ге немесе $s$-ке тең болса, онда бұл тізбекте 1 саны кездеседі.
комментарий/решение
Егер бұл тізбекте 1 саны кездессе, онда $n$ санын $s^2-1$ санына бөлгенде қалдық 1-ге немесе $s$-ке тең екенін дәлелдеңіз, және оған кері қасиетті дәлелдеңіз: егер $n$ санын $s^2-1$ санына бөлгенде қалдық 1-ге немесе $s$-ке тең болса, онда бұл тізбекте 1 саны кездеседі.
комментарий/решение
Есеп №6. $\Omega$ деп $ABC$ үшбұрышына сырттай сызылған шеңберді белгілейік. $S_b$ және $S_c$ — сәйкесінше $AC$ және $AB$ доғаларының (үшінші төбені қамтымайтын бөліктерінің) орталары. $N_a$ — $BAC$ доғасының ортасы (яғни, $A$ төбесін қамтитын $BC$ доғасының ортасы). $I$ — $ABC$ үшбұрышына іштей сызылған шеңбер центрі. $\omega_b$ — $AB$ түзуін жанап, $\Omega$ шеңберін $S_b$ нүктесінде іштей жанайтын шеңбер, ал $\omega_c$ — $AC$ түзуін жанап, $\Omega$ шеңберін $S_c$ нүктесінде іштей жанайтын шеңбер болсын. $IN_a$ түзуі мен $\omega_b$ пен $\omega_c$ шеңберлерінің қиылысу нүктелері арқылы өтетін түзу, $\Omega$-ның бойында қиылысатынын дәлелдеңіз.
комментарий/решение(1)
комментарий/решение(1)