Юниорская олимпиада по математике. Районный этап. 2022-2023 учебный год. 8 класс.
Задача №1. Даны стороны и высота параллелепипеда $a$, $b$, $c$ которые равны 5, 8 и 10. Найдите диагональ параллелепипеда.
A) $3\sqrt{21}$
B) $10\sqrt{3}$
C) 13
D) $9\sqrt{19}$
E) $12\sqrt{2}$
комментарий/решение
A) $3\sqrt{21}$
B) $10\sqrt{3}$
C) 13
D) $9\sqrt{19}$
E) $12\sqrt{2}$
комментарий/решение
Задача №2. Решите ребус: $C,BA+A,AA = B,A.$
A) $A=0$, $B=2$, $C=6$
B) $A=5$, $B=3$, $C=8$
C) $A=5$, $B=9$, $C=3$
D) $A=2$, $B=5$, $C=4$
E) $A=0$, $B=1$, $C=7$
комментарий/решение
A) $A=0$, $B=2$, $C=6$
B) $A=5$, $B=3$, $C=8$
C) $A=5$, $B=9$, $C=3$
D) $A=2$, $B=5$, $C=4$
E) $A=0$, $B=1$, $C=7$
комментарий/решение
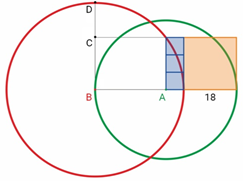
Задача №3. На рисунке ниже: три синие фигуры — квадраты; оранжевая фигура — квадрат со стороной 18; точка $A$ — центр зелёной окружности; точка $B$ — центр красной окружности. Найдите длину отрезка $CD$.
A) 10
B) 14
C) 18
D) 22
E) 12
комментарий/решение
A) 10
B) 14
C) 18
D) 22
E) 12
комментарий/решение
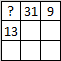
Задача №4. Магический квадрат — это таблица $3 \times 3$, в которой расставлены числа так, что суммы по всем строкам, столбцам и двум главным диагоналям одинаковы. На рисунке изображен магический квадрат, в котором все числа, кроме трёх, стёрты. Найдите, чему равно число в левом верхнем углу квадрата.
A) 14
B) 25
C) 92
D) 12
E) 90
комментарий/решение
A) 14
B) 25
C) 92
D) 12
E) 90
комментарий/решение
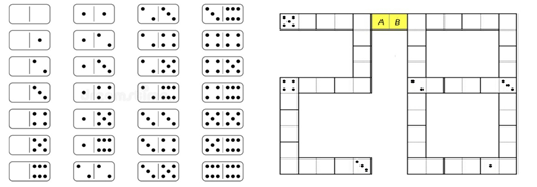
Задача №5. Набор из 28 различных доминошек выглядит так: Все эти 28 доминошек выложили так, что количество точек на соприкасающихся половинках доминошек одинаково. На некоторых половинках полностью стерли количество точек. В итоге получилась конструкция, изображенная на рисунке ниже (пустые половинки могли быть изначально пустыми, а могли содержать какое-то количество точек). Сколько точек на каждой из половинок жёлтой костяшки? Точек на половинке $A$: .... Точек на половинке $B$: ....
A) $A=2, B=4$
B) $A=5, B=6$
C) $A=8, B=2$
D) $A=5, B=2$
E) $A=2, B=5$
комментарий/решение
A) $A=2, B=4$
B) $A=5, B=6$
C) $A=8, B=2$
D) $A=5, B=2$
E) $A=2, B=5$
комментарий/решение
Задача №6. Простое число $p$ таково, что число $p+25$ является седьмой степенью простого числа. Чему может быть равно $p$? Укажите все возможные варианты.
A) 771
B) 299
C) 103
D) 527
E) 1307
комментарий/решение
A) 771
B) 299
C) 103
D) 527
E) 1307
комментарий/решение
Задача №7. Дан тупоугольный треугольник $ABC$ с тупым углом $C$. На его сторонах $AB$ и $BC$ отмечены точки $P$ и $Q$ соответственно так, что $\angle ACP = CPQ = 90^\circ$. Найдите длину отрезка $PQ$, если известно, что $AC = 25$, $CP = 20$, $\angle APC =\angle A+\angle B$.
A) 12
B) 16
C) 20
D) 42
E) 17
комментарий/решение
A) 12
B) 16
C) 20
D) 42
E) 17
комментарий/решение
Задача №8. Упростите выражение: $x^4+7x^3-21x^2-27x.$
A) $(x-1)(x-2)(x+7)x$
B) $(x+1)(x-3)(x+9)$
C) $(x+1)(x-3)(x+9)x$
D) $(x-1)(x+3)(x+9)x$
E) $(x+3)(x-1)(x+9)$
комментарий/решение
A) $(x-1)(x-2)(x+7)x$
B) $(x+1)(x-3)(x+9)$
C) $(x+1)(x-3)(x+9)x$
D) $(x-1)(x+3)(x+9)x$
E) $(x+3)(x-1)(x+9)$
комментарий/решение
Задача №9. Сумма трёх различных натуральных делителей нечётного натурального числа $n$ равна 10327. Какое наименьшее значение может принимать $n$?
A) 10327
B) 15633
C) 8725
D) 6735
E) 9817
комментарий/решение
A) 10327
B) 15633
C) 8725
D) 6735
E) 9817
комментарий/решение
Задача №10. На окружности $\omega$ по разные стороны от диаметра $AC$ расположены точки $B$ и $D$. Известно, что $AB = 3\sqrt{6}$, $CD = 3$, а площадь треугольника $ABC$ в три раза больше площади треугольника $BCD$. Найдите радиус окружности $\omega$.
A) 7
B) 9
C) 3,5
D) 5
E) 4,5
комментарий/решение
A) 7
B) 9
C) 3,5
D) 5
E) 4,5
комментарий/решение
Задача №11. Произведение положительных чисел $a$ и $b$ равно 1. Известно, что $(3a+2b)(3b+2a) = 295$. Найдите $a+b$.
A) 45
B) 12
C) 4
D) 7
E) 47
комментарий/решение
A) 45
B) 12
C) 4
D) 7
E) 47
комментарий/решение
Задача №12. На стороне $AC$ равностороннего треугольника $ABC$ отмечена точка $D$. На отрезках $AD$ и $DC$ во внешнюю сторону от исходного треугольника построены равносторонние треугольники $ADE$ и $DCF$. Известно, что периметр треугольника $DEF$ равен 19, а периметр пятиугольника $ABCFE$ равен 43. Найдите длину отрезка $AB$ и $ЕF$.
A) 12, 5
B) 15, 12
C) 12, 7
D) 7, 15
E) 7, 12
комментарий/решение
A) 12, 5
B) 15, 12
C) 12, 7
D) 7, 15
E) 7, 12
комментарий/решение
Задача №13. В компании некоторые пары людей дружат (если $A$ дружит с $B$, то и $B$ дружит с $A$). Оказалось, что среди каждых 100 человек в компании количество пар дружащих людей нечетно. Найдите наибольшее возможное количество человек в такой компании.
A) 422
B) 263
C) 141
D) 101
E) 100
комментарий/решение
A) 422
B) 263
C) 141
D) 101
E) 100
комментарий/решение
Задача №14. Разложите на множители: $2x^4-2x^2-24.$
A) $(x-2)(x^2+3)(2x+4)$
B) $(x+2)(x+3)(2x-4)$
C) $(x-2)(x^4+3)(2x-4)$
D) $(x-3)(3x-2)(x^3+1)$
E) $(x+2)(x+3)(2x+4)$
комментарий/решение
A) $(x-2)(x^2+3)(2x+4)$
B) $(x+2)(x+3)(2x-4)$
C) $(x-2)(x^4+3)(2x-4)$
D) $(x-3)(3x-2)(x^3+1)$
E) $(x+2)(x+3)(2x+4)$
комментарий/решение
Задача №15. $x$ и $y$ не нулевые действительные числа такие, что $\frac{3x+y}{x-3y}=-2$. Найдите значение выражения $\frac{x+3y}{3x-y}.$
A) $-1$
B) $-3$
C) 1
D) 2
E) 3
комментарий/решение
A) $-1$
B) $-3$
C) 1
D) 2
E) 3
комментарий/решение
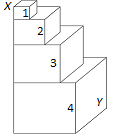
Задача №16. 4 кубика с размерами 1, 2, 3 и 4 расположены как на рисунке ниже. Найдите длину отрезка $XY$ которая проходит через кубик с размером 3.
A) $3\sqrt{33}:5$
B) $2\sqrt{3}$
C) $2\sqrt{33}:3$
D) 4
E) $3\sqrt{2}$
комментарий/решение
A) $3\sqrt{33}:5$
B) $2\sqrt{3}$
C) $2\sqrt{33}:3$
D) 4
E) $3\sqrt{2}$
комментарий/решение
Задача №17. Вычислите: $\frac{2^3+2^3}{2^{-3}+2^{-3}}.$
A) 16
B) 24
C) 32
D) 48
E) 64
комментарий/решение
A) 16
B) 24
C) 32
D) 48
E) 64
комментарий/решение
Задача №18. Мальчик пошел с отцом в тир. Отец купил ему 10 пулек. В дальнейшем отец за каждый промах отбирал у сына одну пульку, а за каждое попадание давал одну дополнительную пульку. Сын выстрелил 55 раз, после чего пульки у него кончились. Сколько раз он попал?
A) 42
B) 55
C) 50
D) 60
E) 65
комментарий/решение
A) 42
B) 55
C) 50
D) 60
E) 65
комментарий/решение
Задача №19. Сколько всего четырёхзначных чисел, которые делятся на 19 и заканчиваются на 19?
A) 24
B) 5
C) 0
D) 1
E) 43
комментарий/решение
A) 24
B) 5
C) 0
D) 1
E) 43
комментарий/решение
Задача №20. Сколько всего пятизначных чисел, которые можно превратить в палиндром, переставивших них цифры местами? (Палиндром-число, которое читается слева направо и справа налево одинакова.)
A) 1000
B) 100
C) 500
D) 900
E) 750
комментарий/решение
A) 1000
B) 100
C) 500
D) 900
E) 750
комментарий/решение
Задача №21. Число $5^{867}$ расположен между $2^{2013}$ и $2^{2014}$. Сколько существует пар $(m, n)$ которые соответствуют этим условиям $1\le m \le 2012$, $5^n < 2^m < 2^{m+2} < 5^{n+1}$?
A) 278
B) 279
C) 280
D) 281
E) 282
комментарий/решение
A) 278
B) 279
C) 280
D) 281
E) 282
комментарий/решение
Задача №22. Сумма двух чисел в 5 раз больше чем их разница. Найдите соотношение большого числа к маленькому.
A) $5:4$
B) $3:2$
C) $9:5$
D) $2:1$
E) $5:2$
комментарий/решение
A) $5:4$
B) $3:2$
C) $9:5$
D) $2:1$
E) $5:2$
комментарий/решение
Задача №23. Найдите последнюю цифру: $2023^{2023}+2^{2023}+3^{2023}.$
A) 7
B) 0
C) 1
D) 2
E) 5
комментарий/решение
A) 7
B) 0
C) 1
D) 2
E) 5
комментарий/решение
Задача №24. $BD$ — биссектриса треугольника $ABC$, $AD = 3$ и $DC = 8$. Найдите наименьший возможный периметр треугольника $ABC$.
A) 30
B) 33
C) 35
D) 36
E) 37
комментарий/решение
A) 30
B) 33
C) 35
D) 36
E) 37
комментарий/решение
Задача №25. В клетках доски $8 \times 8$ расставлены натуральные числа от 1 до 64 (каждое по разу) так, что числа, отличающиеся на 1, стоят в соседних по стороне клетках. Какое наименьшее значение может принимать сумма чисел на диагонали из левого нижнего в правый верхний угол?
A) 8
B) 121
C) 50
D) 88
E) 64
комментарий/решение
A) 8
B) 121
C) 50
D) 88
E) 64
комментарий/решение
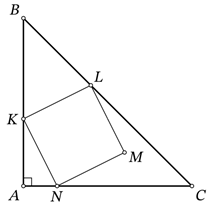
Задача №26. Дан прямоугольный равнобедренный треугольник $ABC$ с прямым углом $A$. Квадрат $KLMN$ расположен, как на рисунке: точки $K, L, N$ лежат на сторонах $AB, BC, AC$ соответственно, а точка $M$ расположена внутри треугольника $ABC$. Найдите длину отрезка $AC$, если известно, что $AK = 7$, $AN = 3$.
A) 15
B) 17
C) 23
D) 25
E) 9
комментарий/решение
A) 15
B) 17
C) 23
D) 25
E) 9
комментарий/решение
Задача №27. У натурального числа $N$ выписали все его делители, затем у каждого из этих делителей подсчитали сумму цифр. Оказалось, что среди этих сумм нашлись все числа от 1 до 9. Найдите наименьшее значение $N$.
A) 144
B) 288
C) 346
D) 502
E) 998
комментарий/решение
A) 144
B) 288
C) 346
D) 502
E) 998
комментарий/решение
Задача №28. Высота $CH$, опущенная из вершины прямого угла треугольника $ABC$, делит биссектрису $BL$ этого треугольника пополам. Найдите угол $BAC$.
A) 90
B) 60
C) 45
D) 30
E) 70
комментарий/решение
A) 90
B) 60
C) 45
D) 30
E) 70
комментарий/решение
Задача №29. Точки $M$ и $N$ — середины сторон $BC$ и $AD$ четырёхугольника $ABCD$. Известно, что $\angle В = 150\circ$, $\angle С = 90\circ$ и $AB = CD$. Найдите угол между прямыми $MN$ и $BC$.
A) 40
B) 30
C) 55
D) 45
E) 60
комментарий/решение
A) 40
B) 30
C) 55
D) 45
E) 60
комментарий/решение
Задача №30. Известно, что $a^2+b = b^2+c = c^2+a$. Какие значения может принимать выражение $(a^2-b^2)+b(b^2-c^2)+c(c^2-a^2)$?
A) 0
B) 1
C) 2
D) 5
E) 10
комментарий/решение
A) 0
B) 1
C) 2
D) 5
E) 10
комментарий/решение