Юниорская олимпиада по математике. Районный этап. 2023-2024 учебный год. 8 класс.
Задача №1. Сколько трёхзначных чисел делятся на 12, 16 и 18 одновременно?
A) 8
B) 7
C) 6
D) 5
E) 9
комментарий/решение
A) 8
B) 7
C) 6
D) 5
E) 9
комментарий/решение
Задача №2. Сколькими различными способами можно представить число в виде 24 произведения $x\cdot y \cdot z$, где $x$, $y$ и $z$ — натуральные числа.
A) 24
B) 30
C) 12
D) 36
E) 28
комментарий/решение
A) 24
B) 30
C) 12
D) 36
E) 28
комментарий/решение
Задача №3. В очереди в школьную столовую стоят 16 школьников так, что мальчики и девочки среди них чередуются. (Первым стоит мальчик, за ним — девочка, за ней — снова мальчик и так далее.) Любой мальчик, за которым в очереди стоит девочка, может поменяться с ней местами. Через некоторое время оказалось, что все девочки стоят в начале очереди, а все мальчики — в конце. Сколько обменов было совершено?
A) 32
B) 34
C) 36
D) 38
E) 37
комментарий/решение
A) 32
B) 34
C) 36
D) 38
E) 37
комментарий/решение
Задача №4. Данная фигура склеена из кубиков размером $1 \times 1 \times 1$. Чему равна площадь поверхности этой фигуры?
A) 36
B) 30
C) 28
D) 32
E) 26
комментарий/решение

A) 36
B) 30
C) 28
D) 32
E) 26
комментарий/решение
Задача №5. В роще растут деревья четырёх видов: березы, ели, сосны и осины. Всего 100 деревьев. Известно, что среди любых 85 деревьев найдутся деревья всех четырёх видов. Среди какого наименьшего количества любых деревьев в этой роще обязательно найдутся деревья хотя бы трёх видов?
A) 56
B) 72
C) 85
D) 58
E) 69
комментарий/решение
A) 56
B) 72
C) 85
D) 58
E) 69
комментарий/решение
Задача №6. Асхат загадал трёхзначное число, а Даулет пытается его угадать. Даулет по очереди назвал числа 109, 704 и 524. Аcхат заметил, что каждое из этих чисел совпадает с загаданным числом ровно в одном разряде. Какое число загадал Асхат?
A) 209
B) 279
C) 709
D) 729
E) 592
комментарий/решение
A) 209
B) 279
C) 709
D) 729
E) 592
комментарий/решение
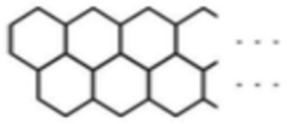
Задача №7. У Максата есть 2023 спички. Он выкладывает из них в два ряда шестиугольники, примыкающие друг к другу. Сколько шестиугольников у него получится?
A) 505
B) 504
C) 506
D) 503
E) 501
комментарий/решение
A) 505
B) 504
C) 506
D) 503
E) 501
комментарий/решение
Задача №8. Если продолжить пирамиду, то какое число будет записано прямо под числом 101?
A) 123
B) 120
C) 121
D) 119
E) 128
комментарий/решение

A) 123
B) 120
C) 121
D) 119
E) 128
комментарий/решение
Задача №9. У бабушки была скатерть размером $7 \times 7$. Когда бабушка достала скатерть, то она увидела, что часть скатерти съела мышь. То что съела мышь помечено чёрным цветом на рисунке. Бабушка решила вырезать из испорченной скатерти как можно больше салфеток $1 \times 2$. Какое наибольшее количество салфеток сможет получить бабушка?
A) 20
B) 24
C) 16
D) 18
E) 19
комментарий/решение

A) 20
B) 24
C) 16
D) 18
E) 19
комментарий/решение
Задача №10. Дано выражение $\text{МАТЕМ} + \text{АТИКА}$, где каждая буква обозначает цифру, причем разные буквы обозначают разные цифры. Чему равно наименьшее значение этого выражения?
A) 23218
B) 34184
C) 41385
D) 31393
E) 42341
комментарий/решение
A) 23218
B) 34184
C) 41385
D) 31393
E) 42341
комментарий/решение
Задача №11. Найдите 2023-ую цифру после запятой в десятичном разложении дроби 5/14.
A) 3
B) 2
C) 8
D) 7
E) 9
комментарий/решение
A) 3
B) 2
C) 8
D) 7
E) 9
комментарий/решение
Задача №12. Очевидно, что равенство $\frac{23}{30}=\frac{57}{78}$ неверно. Однако если из каждого из 23, 30, 57 и 78 вычесть одно и то же положительное целое число, то это будет правильно. Какое число нужно вычесть?
A) 6
B) 5
C) 11
D) 8
E) 10
комментарий/решение
A) 6
B) 5
C) 11
D) 8
E) 10
комментарий/решение
Задача №13. Сколько натуральных делителей у числа $2023^3$?
A) 28
B) 24
C) 18
D) 21
E) 19
комментарий/решение
A) 28
B) 24
C) 18
D) 21
E) 19
комментарий/решение
Задача №14. Дан треугольник $A B C$. Биссектрисы внутренних углов $C A B$ и $C B A$ пересекаются в точке $P$. Найдите угол $\angle A P B$, если известно, что $\angle A C B=36$?
A) $72^\circ$
B) $108^\circ$
C) $126^\circ$
D) $136^\circ$
E) $106^\circ$
комментарий/решение
A) $72^\circ$
B) $108^\circ$
C) $126^\circ$
D) $136^\circ$
E) $106^\circ$
комментарий/решение
Задача №15. В последовательности $72469106635042174\ldots$ каждая цифра, начиная с пятой, равна последней цифре суммы четырех предшествующих цифр. Какая из следующих четверок не встретится в этой последовательности?
A) 2023
B) 8192
C) 1569
D) 2024
E) 3027
комментарий/решение
A) 2023
B) 8192
C) 1569
D) 2024
E) 3027
комментарий/решение
Задача №16. Алдар Косе, Ер Тостик и Кыз Жибек вышли с олимпиады. Сколькими способами можно выставить им баллы за олимпиаду (от 0 до 21) так, чтобы у Кыз Жибека было баллов больше, чем у Ер Тостика, а у Ер Тостика — больше, чем у Алдар Косе?
A) 3080
B) 1330
C) 3990
D) 2620
E) 1540 или 3070
комментарий/решение
A) 3080
B) 1330
C) 3990
D) 2620
E) 1540 или 3070
комментарий/решение
Задача №17. В остроугольном треугольнике $ABC$ проведены медиана $BM$ и высота $CH$. Найдите длину $AC$, если $MH = 10$ см.
A) 10 см
B) 15 см
C) 20 см
D) 25 см
E) 16 см
комментарий/решение
A) 10 см
B) 15 см
C) 20 см
D) 25 см
E) 16 см
комментарий/решение
Задача №18. В хоре более 2/5, но менее 1/2 детей — мальчики. Какое наименьшее возможное количество детей в этом хоре?
A) 5
B) 7
C) 9
D) 4
E) 8
комментарий/решение
A) 5
B) 7
C) 9
D) 4
E) 8
комментарий/решение
Задача №19. В треугольнике $A B C \angle A B C=\angle A C B=30^{\circ}$. $O$ - точка такая, что $O A=O C=1$ см и $O B=2$ см. Более того, $\angle C A B=\angle C A O+\angle O A B$. Какова длина $BC$?
A) 1,5 см
B) 2 см
C) 3 см
D) 2,5 см
E) 3,5 см
комментарий/решение
A) 1,5 см
B) 2 см
C) 3 см
D) 2,5 см
E) 3,5 см
комментарий/решение
Задача №20. Найдите разность чисел $1234567891 \times 1234567896 \times 1234567898$ и $1234567899 \times 1234567894 \times 1234567892$.
A) 20
B) 24
C) 30
D) 23
E) 32
комментарий/решение
A) 20
B) 24
C) 30
D) 23
E) 32
комментарий/решение
Задача №21. Мы считаем сумму цифр числа $2023^{2024}$. Потом считаем сумму цифр получившегося числа. И так далее пока в конце не останется одна цифра. Найдите эту цифру.
A) 2
B) 4
C) 7
D) 5
E) 8
комментарий/решение
A) 2
B) 4
C) 7
D) 5
E) 8
комментарий/решение
Задача №22. Произведение пяти целых положительных чисел равно 2023. Сколько различных значений может получить их сумма?
A) 6
B) 5
C) 8
D) 7
E) 4
комментарий/решение
A) 6
B) 5
C) 8
D) 7
E) 4
комментарий/решение
Задача №23. Дан прямоугольник $ABCD$ . $E$ — середина $BC$, а $F$ — середина $CD$. $BD$ пересекает $AE$ в точке $M$ и $AF$ в точке $N$. Если $AB=12$ см и $AD=5$ см, какова длина $M N$?
A) 4
B) $\frac{11}{3}$
C) $\frac{13}{3}$
D) 5
E) $\frac{10}{3}$
комментарий/решение
A) 4
B) $\frac{11}{3}$
C) $\frac{13}{3}$
D) 5
E) $\frac{10}{3}$
комментарий/решение
Задача №24. На вечеринке каждые два человека пожимают друг другу руки, кроме Алмата, который пожимает руки только некоторым людям. Никакие два человека не пожимают друг другу руки более одного раза. Если общее количество рукопожатий равно 2023, скольким людям Алмат пожимает руки?
A) 21
B) 15
C) 12
D) 7
E) 19
комментарий/решение
A) 21
B) 15
C) 12
D) 7
E) 19
комментарий/решение
Задача №25. Кошка поймала в три раза больше черных мышей, чем белых. Каждый день она съедает 6 черных и 4 белых мышей. Через несколько дней осталось 60 черных мышей и 4 белых мыши. Сколько мышей поймал кот?
A) 120
B) 152
C) 116
D) 148
E) 144
комментарий/решение
A) 120
B) 152
C) 116
D) 148
E) 144
комментарий/решение
Задача №26. На какое количество нулей оканчиваться число $1^{2023} + 2^{2023} + 3^{2023} + 4^{2023}$?
A) 3
B) 2
C) 1
D) 0
E) 4
комментарий/решение
A) 3
B) 2
C) 1
D) 0
E) 4
комментарий/решение
Задача №27. У скольких девятизначных чисел все цифры различны, сумма каждой пары соседних цифр нечетна, а само число делится на 4?
A) 4320
B) 5760
C) 14400
D) 11520
E) 2360
комментарий/решение
A) 4320
B) 5760
C) 14400
D) 11520
E) 2360
комментарий/решение
Задача №28. На доске написаны обратные значения первых 2023 натуральных чисел. За один ход мы можем стереть два числа и заменить их суммой их суммы и их произведения (то есть, вместо $a$ и $b$ напишем $a+b+a b)$. В конце концов остается только одно число. Каково максимальное значение этого числа?
A) 2030
B) 2024
C) 2020
D) 2023
E) 2027
комментарий/решение
A) 2030
B) 2024
C) 2020
D) 2023
E) 2027
комментарий/решение
Задача №29. Команду выбирают из 4 девочек и 6 мальчиков. Единственное требование — в нем должно быть минимум 2 девушки. Сколько разных команд можно выбрать?
A) 640
B) 512
C) 576
D) 704
E) 610
комментарий/решение
A) 640
B) 512
C) 576
D) 704
E) 610
комментарий/решение
Задача №30. Для окраски шести граней куба есть пять цветов. Один цвет используется для рисования двух граней, а каждый из остальных четырех цветов используется для рисования одной грани. Сколько может быть кубиков, окрашенных в разные цвета? Два кубика, окрашивающие соответствующие грани в одинаковые цвета после поворота или переворота, не считаются разными.
A) 75
B) 70
C) 80
D) 95
E) 90
комментарий/решение
A) 75
B) 70
C) 80
D) 95
E) 90
комментарий/решение