Фольклор
Задача №1. Определите множество целых значений выражения $\dfrac{{a + 1}}{b} + \dfrac{{b + 1}}{a}$ для натуральных $a$ и $b$. ( Фольклор )
комментарий/решение(1) олимпиада
Задача №2. На стороне $AB$ равнобедренного треугольника $ABC$ ($AC=BC$) отмечены точки $P$ и $Q$ такие, что $\angle PCQ\leq{1\over 2}\angle ACB$. Докажите, что $PQ\leq{1\over 2}AB$. ( Фольклор )
комментарий/решение(3) олимпиада
Задача №3. Могут ли три человека, имея один двухместный мотоцикл, преодолеть расстояние 70 км за 3 часа? Скорость пешехода 5 км/ч, скорость мотоцикла — 50 км/ч. ( Фольклор )
комментарий/решение олимпиада
Задача №4. Фокусник просит зрителя задумать трехзначное число $\overline{abc}$, а затем назвать ему сумму чисел $\overline{acb}$, $\overline{bac}$, $\overline{bca}$, $\overline{cab}$ и $\overline{cba}$. Он утверждает, что узнав эту сумму, сможет назвать исходное число. Не обманывает ли он? ( Фольклор )
комментарий/решение(2) олимпиада
Задача №5. В клетках доски, изображенной на рисунке, стоят несколько ладей, которые бьют все клетки (считается, что ладья бьет клетку, на которой стоит). Докажите, что можно убрать несколько ладей, оставив не более 11, так, чтобы оставшиеся ладьи по-прежнему били все клетки.
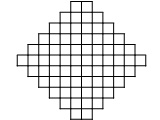
комментарий/решение олимпиада
Задача №6. За круглым столом сидели 99 человек, каждый из которых либо рыцарь, который всегда говорит правду, либо лжец, который всегда лжёт. Каждый из них сказал: «Хотя бы один из двух моих соседей — лжец.» Могло ли среди них быть ровно 60 рыцарей? ( Фольклор )
комментарий/решение(2) олимпиада
Задача №7. Велосипедисты Андрей, Борис и Виктор одновременно, из одной точки и в одном направлении стартовали по кольцевой дороге. Каждый из них ехал с постоянной скоростью, причем у разных велосипедистов скорости были различными. Андрей впервые перегнал Бориса, проехав ровно четыре круга, а Виктора — проехав ровно пять кругов. Сколько кругов проехал Виктор к моменту, когда он впервые обогнал Бориса? ( Фольклор )
комментарий/решение(1) олимпиада
Задача №8. На дискотеку пришли 42 человека: мальчики и девочки. Каждая девочка потанцевала со всеми мальчиками, кроме четырёх, а каждый мальчик потанцевал со всеми девочками, кроме трёх. Сколько мальчиков было на танцах? ( Фольклор )
комментарий/решение(10) олимпиада
Задача №9. Семь различных камней таковы, что любые шесть из них вместе весят меньше 6 кг. Докажите, что все семь камней вместе весят меньше 7 кг. ( Фольклор )
комментарий/решение(6) олимпиада
Задача №10. Мотоциклист был в пути три часа (какое-то время он мог и стоять). Его средняя скорость в первые два часа равнялась 50 км/ч и в последние два часа — тоже 50 км/ч. Какое наибольшее расстояние он мог преодолеть? ( Фольклор )
комментарий/решение олимпиада