Олимпиада Туймаада по математике. Старшая лига. 2023 год
Задача №1. В узлах клетчатой решетки по спирали расставляют числа $1,2,3 \ldots$ (см. рисунок). Потом в центре каждой клетки пишут сумму чисел в ее узлах. Докажите, что для любого натурального $n$ в центрах клеток бесконечно много раз встретятся числа, делящиеся на $n$.
комментарий/решение
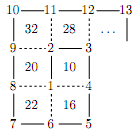
комментарий/решение
Задача №2. В графе с $n$ вершинами каждые две вершины соединены единственным путём. Для каждых двух вершин $u$ и $v$ обозначим через $d(u, v)$ расстояние между $u$ и $v$, т. е. количество ребер в пути, соединяющем эти вершины, а через $\deg u$ обозначим степень вершины $u$. Пусть $W$ — сумма всех попарных расстояний между вершинами, $D$ — сумма всех взвешенных попарных расстояний: $$ D=\sum_{\{u, v\}}(\deg u+\deg v) d(u, v).$$ Докажите, что $D=4 W-n(n-1)$.
(
I. Gutman
)
комментарий/решение
комментарий/решение
Задача №3. Докажите что при натуральных $n \geqslant 2$ выполняется неравенство: $$ \frac{\sqrt[3]{\frac{1}{n+1}}+\sqrt[3]{\frac{2}{n+1}}+\ldots+\sqrt[3]{\frac{n}{n+1}}}{n} \leqslant \frac{\sqrt[3]{\frac{1}{n}}+\sqrt[3]{\frac{2}{n}}+\ldots+\sqrt[3]{\frac{n-1}{n}}}{n-1}.$$
(
J. Liu
)
комментарий/решение
комментарий/решение
Задача №4. На плоскости даны точки $A$ и $B$, а также прямая $\ell$, не перпендикулярная $A B$ и не пересекающая отрезок $A B$. Рассматриваются всевозможные окружности с центрами $O \notin \ell$, проходящие через точки $A$ и $B$ и пересекающие $\ell$ в двух точках — обозначим эти точки $C$ и $D$. Докажите, что все описанные окружности треугольников $O C D$ касаются одной и той же фиксированной окружности.
(
С. Берлов
)
комментарий/решение
комментарий/решение
Задача №5. По бесконечному координатному морю плавает кораблик. В момент времени $t$ кораблик находится в точке с координатами $(f(t), g(t))$, где $f$ и $g$ — два многочлена третьей степени. Вчера в 14:00 кораблик оказался там же, где был в 13:00, а в 20:00 — там же, где был в 19:00. Докажите, что кораблик плавает по прямой.
(
А. Голованов
)
комментарий/решение
комментарий/решение
Задача №6. На плоскости нарисовано $n$ отрезков, длины которых равны $a_1$, $a_2, \ldots, a_n$. Любой луч, выходящий из точки $O$, пересекает хотя бы один отрезок. Пусть $h_i$ — это расстояние от точки $O$ до отрезка (не до прямой!) с номером $i$. Докажите неравенство: $$ \frac{a_1}{h_1}+\frac{a_2}{h_2}+\ldots+\frac{a_n}{h_n} \geqslant 2 \pi. $$
(
Ф. Бахарев
)
комментарий/решение
комментарий/решение
Задача №7. Есть гексагональная доска со стороной $n$ клеток, на ее клетках лежат шестиугольные плитки, пронумерованные натуральными числами. Две соседние клетки доски оставлены пустыми, благодаря чему плитки можно двигать. Две соседние по стороне плитки поменяли местами (см. пример на рисунке). Докажите, что при $n \geqslant 3$, двигая плитки, не удастся из первого положения получить второе. Примечание. Чтобы подвинуть плитку $a$, рядом должны находиться две пустые клетки. Например, если они расположены справа от плитки $a$ (левый рис.), мы можем подвинуть плитку $a$ вправо, пока она не упрется углом (рис. в центре), после чего ее можно сдвинуть вправо вверх или вправо вниз (рис. справа).
(
E. Roldan,
R. Karpman
)
комментарий/решение
комментарий/решение
Задача №8. Дано натуральное число $n$. Пусть $A$ — множество точек $x$ интервала $(0,1)$ таких, что $\left|x-\frac{p}{q}\right|>\frac{1}{n^3}$ для любой рациональной дроби $\frac{p}{q}$ со знаменателем $q \leqslant n^2$. Докажите, что $A$ представляет собой объединение интервалов суммарной длины не более $\frac{100}{n}$.
(
Ф. Петров
)
комментарий/решение
комментарий/решение