Олимпиада Туймаада по математике. Старшая лига. 2023 год
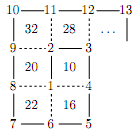
Есеп №1. Ұяшықтары бар тор түйіндеріне $1,2,3 \ldots$ сандары спираль бойымен жазылады (суретті қараңыз). Кейін әр ұяшықтың ортасына оның төбелеріндегі сандардың қосындысы жазылады. Кез келген натурал $n$ үшін ұяшықтардың ортасында шексіз көп рет $n$-ге бөлінетін сандар пайда болатынын дәлелдеңіз.
комментарий/решение
комментарий/решение
Есеп №2. $n$ төбесі бар графта кез келген екі төбе жалғыз жолмен қосылған. Кез келген $u$ және $v$ төбелері үшін $d(u,v)$ деп $u$ мен $v$ арасындағы жолдағы қырлар санын, ал $\deg u$ деп $u$ төбесінің дәрежесін белгілейік. $W$ — барлық төбе жұптарының арақашықтықтарының қосындысы, ал $D$ — барлық салмақталған арақашықтықтардың қосындысы: $$ D=\sum_{\{u, v\}}(\deg u+\deg v)\, d(u, v). $$ $D=4W-n(n-1)$ екенін дәлелдеңіз.
(
I. Gutman
)
комментарий/решение
комментарий/решение
Есеп №3. Натурал $n\ge2$ сандары үшін келесі теңсіздік орындалатынын дәлелдеңіз: $$ \frac{\sqrt[3]{\frac{1}{n+1}}+\sqrt[3]{\frac{2}{n+1}}+\ldots+\sqrt[3]{\frac{n}{n+1}}}{n}\le\frac{\sqrt[3]{\frac{1}{n}}+\sqrt[3]{\frac{2}{n}}+\ldots+\sqrt[3]{\frac{n-1}{n}}}{n-1}. $$
(
J. Liu
)
комментарий/решение
комментарий/решение
Есеп №4. Жазықтықта $A$ және $B$ нүктелері, сондай-ақ $A B$ кесіндісіне перпендикуляр емес және оны қимайтын $\ell$ түзуі берілген. $A$ және $B$ нүктелері арқылы өтетін және центрі $O\notin \ell$ болатын барлық шеңберлер қарастырылады; олар $\ell$ түзуін $C$ және $D$ нүктелерінде қияды. $O C D$ үшбұрыштарының сырттай сызылған шеңберлері бір тұрақты шеңбермен жанасатынын дәлелдеңіз.
(
С. Берлов
)
комментарий/решение
комментарий/решение
Есеп №5. Шексіз координаттық теңізде қайық жүзіп жүр. Уақыт $t$ кезінде қайықтың координаттары $(f(t), g(t))$, мұнда $f$ және $g$ — үшінші дәрежелі көпмүшелер. Кеше 13:00-де қайық қай жерде тұрса, 14:00-де де сол жерде тұрды, ал 19:00-де тұрған жерінде 20:00-де де болды. Қайық түзу бойымен жүзіп жүргенін дәлелдеңіз.
(
А. Голованов
)
комментарий/решение
комментарий/решение
Есеп №6. Жазықтықта ұзындықтары $a_1,a_2,\ldots,a_n$ болатын $n$ кесінді салынған. Кез келген $O$ нүктесінен шыққан сәуле кемінде бір кесіндіні қияды. $h_i$ — $O$ нүктесінен $i$-ші кесіндінің өзіне дейінгі қашықтық (түзуге емес!). Келесі теңсіздікті дәлелдеңіз: $$ \frac{a_1}{h_1}+\frac{a_2}{h_2}+\ldots+\frac{a_n}{h_n}\ge2\pi. $$
(
Ф. Бахарев
)
комментарий/решение
комментарий/решение
Есеп №7. Ұяшықтары гексагональ тақташада, оның қабырғасы $n$ ұяшықтан тұрады, ұяшықтарда табиғи сандармен нөмірленген алтыбұрышты плиткалар жатыр. Тақтада екі көршілес ұяшық бос қалған, сол себепті плиткаларды қозғалтуға болады. Екі көршілес плитка орын алмастырды (мысал суретте). Егер $n\ge3$ болса, плиткаларды қозғау арқылы бірінші орналасудан екіншісіне өту мүмкін емес екенін дәлелдеңіз. Ескерту. Плитканы қозғалту үшін оның жанында екі бос ұяшық болуы керек. Мысалы, егер олар плитканың оң жағында орналасса (сол жақ сурет), плитканы оңға қарай жылжытып, бұрышқа дейін апаруға болады (орталық сурет), сосын оны оңға жоғары немесе оңға төмен жылжытуға болады (оң жақ сурет).
(
E. Roldan,
R. Karpman
)
комментарий/решение
комментарий/решение
Есеп №8. Натурал $n$ саны берілген. $(0,1)$ аралығында $A$ жиыны — сондай $x$ нүктелері, сонда кез келген $q\le n^2$ болатын бөлшек $\frac{p}{q}$ үшін $$\left|x-\frac{p}{q}\right|>\frac{1}{n^3}.$$ $A$ жиыны интервалдардың бірігуі болып табылатынын және олардың жалпы ұзындығы $\frac{100}{n}$-нен аспайтынын дәлелдеңіз.
(
Ф. Петров
)
комментарий/решение
комментарий/решение