И. Рубанов
Задача №1. На столе лежат 7 карточек с цифрами от 0 до 6. Двое по очереди берут по одной карточке. Выигрывает тот, кто впервые из своих карточек сможет составить натуральное число, делящееся на 17. Кто выиграет при правильной игре — начинающий или его противник? ( И. Рубанов )
комментарий/решение(2) олимпиада
Задача №2. На столе лежит 10 кучек с 1, 2, 3, 4, 5, 6, 7, 8, 9 и 10 орехами. Двое играющих берут по очереди по одному ореху. Игра заканчивается, когда на столе останется 3 ореха. Если это — три кучки по одному ореху, выигрывает тот, кто ходил вторым, иначе — его соперник. Кто из игроков может выигрывать, как бы не играл соперник? ( И. Рубанов, А. Шаповалов )
комментарий/решение(2) олимпиада
Задача №3. Однажды барон Мюнхгаузен, вернувшись с прогулки, рассказал, что половину пути он шёл со скоростью 5 км/ч, а половину времени, затраченного на прогулку — со скоростью 6 км/ч. Не ошибся ли барон? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №4. На доске нарисованы три четырёхугольника. Петя сказал: «На доске нарисованы по крайней мере две трапеции». Вася сказал: «На доске нарисованы по крайней мере два прямоугольника». Коля сказал: «На доске нарисованы по крайней мере два ромба». Известно, что один из мальчиков сказал неправду, а двое других — правду. Докажите, что среди нарисованных на доске четырёхугольников есть квадрат. (Напомним, что трапеция — это четырёхугольник, у которого две стороны параллельны, а две другие — нет.) ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №5. На доске написано число 1. Если на доске написано число $a$, его можно заменить любым числом вида $a+d$, где $d$ взаимно просто с $a$ и $10 \leq d \leq 20$. Можно ли через несколько таких операций получить на доске число $18! = 1 \cdot 2 \cdot 3 \cdot \dots \cdot 18$? ( И. Рубанов )
комментарий/решение(4) олимпиада
Задача №6. Для четырёх различных целых чисел подсчитали все их попарные суммы и попарные произведения. Полученные суммы и произведения выписали на доску. Какое наименьшее количество различных чисел могло оказаться на доске? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №7. Каждый из 10 гномов — либо рыцарь, всегда говорящий правду, либо лжец, который всегда врёт, причём хотя бы один из гномов — рыцарь. Все гномы выстроились в шеренгу, после чего девятеро сказали: «Среди стоящих слева от меня есть рыцарь», а оставшийся, Глоин, сказал: «Среди стоящих справа от меня есть рыцарь». Правду сказал Глоин или солгал? ( И. Рубанов )
комментарий/решение(2) олимпиада
Задача №8. На окружности отметили 2013 точек и каждую соединили с двумя соседними. Также отметили центр окружности и соединили его со всеми остальными отмеченными точками. Можно ли покрасить 1007 отмеченных точек в красный, а остальные 1007 — в синий цвет так, чтобы каждая красная точка была соединена с нечётным числом синих, а каждая синяя — с чётным числом синих? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №9. Дано 2014 попарно различных натуральных чисел таких, что произведение любых двух из них делится на сумму этих двух чисел. Докажите, что ни одно из данных чисел не может быть равно произведению шести попарно различных простых чисел. ( И. Рубанов, С. Берлов, В. Сендеров )
комментарий/решение(1) олимпиада
Задача №10. Докажите, что в разложение произведения десяти последовательных трёхзначных чисел на простые множители входит не больше 23 различных простых чисел. ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №11. На доске написаны четыре числа, ни одно из которых не равно 0. Если каждое из них умножить на сумму трёх остальных, получатся четыре одинаковых результата. Докажите, что квадраты записанных на доске чисел равны. ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №12. На столе лежит палочка длиной 10 см. Петя ломает её на две части и кладёт обе получившиеся палочки на стол. С одной из лежащих на столе палочек Вася проделывает ту же операцию, потом то же делает Петя и т.д., по очереди. Петя хочет, чтобы после 18 разломов все получившиеся палочки были короче 1 см. Вася хочет помешать Пете. Кто из них имеет возможность добиться своей цели независимо от действий соперника? ( И. Рубанов, С. Берлов )
комментарий/решение(1) олимпиада
Задача №13. Можно ли за каждую цифру от 0 до 9 назначить цену так, чтобы все 10 цен были различны и нашлись 20 идущих подряд натуральных чисел, каждое из которых, кроме первого, стоит дороже предыдущего? Здесь цена натурального числа — это сумма цен цифр в его записи. ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №14. 10 бегунов стартуют одновременно: пятеро в синих майках с одного конца беговой дорожки, пятеро в красных майках — с другого. Их скорости постоянны и различны, причём скорость каждого бегуна больше 9 км/ч, но меньше 12 км/ч. Добежав до конца дорожки, каждый бегун сразу бежит назад, а, вернувшись к месту своего старта, заканчивает бег. Тренер ставит в блокноте галочку каждый раз, когда встречаются (лицом к лицу или один догоняет другого) двое бегунов в разноцветных майках (больше двух бегунов в одной точке за время бега не встречались). Сколько галочек поставит тренер к моменту, когда закончит бег самый быстрый из бегунов? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №15. В треугольнике $ABC$ провели биссектрису $BD$, а в треугольниках $ABD$ и $CBD$ биссектрисы $DE$ и $DF$ соответственно. Оказалось, что $EF \parallel AC$. Найдите угол $DEF$. ( И. Рубанов )
комментарий/решение(2) олимпиада
Задача №16. Для каждой пары различных натуральных чисел $a$ и $b$, не больших 20, Петя нарисовал на доске прямую $y = ax+b$ (то есть он нарисовал прямые $y = x+2, \ldots , y = x+20,$ $y = 2x+1, y = 2x+3,$ $\ldots,$ $y = 2x+20,$ $\ldots,$ $y = 3x+1, y = 3x+2, y = 3x+4,$ $\ldots,$ $y = 3x+20,$ $\ldots , y = 20x+1, \ldots , y = 20x+19).$ Вася нарисовал на той же доске окружность радиуса 1 с центром в начале координат. Сколько Петиных прямых пересекает Васину окружность? ( И. Рубанов )
комментарий/решение(2) олимпиада
Задача №17. Квадрат со стороной 100 разрезали на квадраты (не обязательно одинаковые) со сторонами, параллельными сторонам исходного квадрата и меньшими 10. Докажите, что сумма периметров получившихся квадратов не меньше 4400. ( И. Рубанов )
комментарий/решение(3) олимпиада
Задача №18. На каждой из пяти карточек написано какое-то число. Карточки лежат на столе числами вниз. Мы можем, заплатив рубль, указать на любые три карточки, и нам сообщат сумму написанных на них чисел. За какую наименьшую цену можно наверняка узнать сумму всех пяти чисел? ( И. Рубанов )
комментарий/решение(2) олимпиада
Задача №19. Четыре мальчика заглянули в коробку, где лежат цветные шарики. На вопрос, каких цветов шарики там лежат, они ответили так. Петя: «Красные, синие и зелёные». Вася: «Красные, синие и жёлтые». Коля: «Красные, жёлтые и зелёные». Миша: «Жёлтые, зелёные и синие». Могло ли случиться, что каждый из мальчиков один цвет назвал верно, а два — неверно? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №20. Боря нарисовал девять отрезков, три из которых равны трём высотам треугольника $ABC$, три — трём биссектрисам, три — трём медианам. Оказалось, что для любого из нарисованных отрезков среди остальных восьми найдётся равный ему. Докажите, что треугольник $ABC$ — равнобедренный. ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №21. По окружности красным карандашом записали 49 различных натуральных чисел, меньших 100. Между каждыми двумя соседними красными числами записали синим их наибольший общий делитель. Могло ли случиться, что все синие числа различны? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №22. В полдень Вася положил на стол 10 вырезанных из бумаги выпуклых десятиугольников. Затем он время от времени брал ножницы, разрезал по прямой один из лежащих на столе многоугольников на два и клал оба получившихся куска назад на стол. К полуночи Вася проделал такую операцию 51 раз. Докажите, что в полночь среди лежащих на столе многоугольников был треугольник или четырёхугольник. ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №23. Из клетчатой доски размером $70 \times 70$ вырезали 2018 клеток. Докажите, что доска распалась не более чем на 2018 кусков. Два куска, не имеющие общих точек кроме вершин клеток, считаются не соединёнными друг с другом. ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №24. Машина едет с постоянной скоростью в одном направлении по прямой дороге, возле которой стоят два дома. В полдень, когда машина еще не доехала до домов, сумма расстояний от нее до этих домов равнялась 10 км. Через 10 минут, когда машина уже миновала оба дома, оказалось, что сумма расстояний от нее до домов снова равна 10 км. Какова скорость машины? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №25. При каком наибольшем натуральном $k$ клетки таблицы $5\times 5$ можно заполнить нулями и единицами (в каждой клетке должно стоять ровно одно число) так, чтобы нашлись $k$ строк, в каждой из которых сумма чисел не меньше 3, и $k$ столбцов, в каждом из которых сумма чисел не больше 2? ( И. Рубанов, О. Нечаева )
комментарий/решение(1) олимпиада
Задача №26. Найдите все натуральные числа $n$, для которых число $n^7+n^6+n^5+1$ имеет ровно три натуральных делителя. ( И. Рубанов, О. Нечаева )
комментарий/решение(1) олимпиада
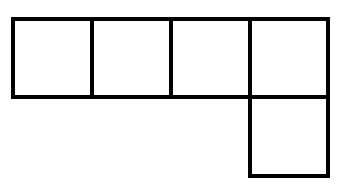
Задача №27. Назовем сапогом клетчатую фигуру, составленную из прямоугольника шириной одну и длиной не менее двух клеток и клетки, примыкающей сбоку к одной из крайних клеток этого прямоугольника (на рисунке изображен пример сапога, составленного из 5 клеток; фигуры, которые получаются из изображенного сапога поворотами и переворотами — тоже сапоги). Можно ли какой-нибудь клетчатый квадрат разрезать по границам клеточек на сапоги, среди которых нет равных? Напомним, что фигуры называются равными, если их можно наложить друг на друга так, что они совместятся.
комментарий/решение(1) олимпиада
Задача №28. Вася, Петя и Коля учатся в одном классе. Вася в ответ на любой вопрос врёт, Петя попеременно врёт и говорит правду, а Коля врёт в ответ на каждый третий вопрос, а в остальных случаях говорит правду. Однажды каждого из них шесть раз подряд спросили, сколько человек учится в их классе. В ответ пять раз прозвучало: «Двадцать пять», шесть раз: «Двадцать шесть» и семь раз: «Двадцать семь». Можно ли по их ответам узнать, сколько человек в их классе на самом деле? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №29. Петя задумал 8 различных чисел, а потом стал выбирать из них по два и делить большее на меньшее. Он нашел 22 из 28 возможных частных, и они оказались натуральными степенями двойки. Докажите, что 6 оставшихся частных — тоже натуральные степени двойки. (Натуральная степень двойки — это 2 в степени, показатель которой равен натуральному числу.) ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №30. На окружности отмечены 48 точек, делящих ее на равные дуги. Играют двое, ходят по очереди. За один ход разрешается стереть либо три отмеченные точки, лежащие в вершинах равностороннего треугольника, либо четыре отмеченные точки, лежащие в вершинах квадрата. Кто при правильной игре выиграет независимо от действий соперника: тот, кто делает первый ход, или тот, кто ходит вторым? ( И. Рубанов, Д. Ширяев )
комментарий/решение(1) олимпиада
Задача №31. Даны два числа (не обязательно целых), не равные 0. Если каждое из них увеличить на единицу, их произведение увеличится вдвое. А во сколько раз увеличится их произведение, если каждое из исходных чисел возвести в квадрат и затем уменьшить на единицу? ( И. Рубанов, Д. Ширяев )
комментарий/решение(1) олимпиада
Задача №32. Графики линейных функций $y = ax+c,$ $y = ax+d,$ $y = bx+e,$ $y = bx+f$ пересекаются в вершинах квадрата $P.$ Могут ли точки $K(a, c),$ $L(a, d),$ $M(b, e),$ $N(b, f)$ располагаться в вершинах квадрата, равного квадрату $P$? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №33. Петя задумал натуральное число, не большее 4. Вася может указать любое натуральное число или несколько чисел и спросить Петю, есть ли задуманное число среди них (например: «Верно ли, что задуманное число равно 2?» или «Верно ли, что задуманное число равно 2 или 3?»). Петя должен ответить «Да» или «Нет». Как Васе за 11 вопросов узнать задуманное число, если Петя в ответ может и соврать, но не больше трех раз? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №34. Напомним, что факториалом $n!$ натурального числа $n$ называется произведение всех натуральных чисел от 1 до $n$ включительно (например, $1! = 1,$ а $5! = 1\cdot 2\cdot 3\cdot 4\cdot 5).$ Можно ли из чисел $1!,$ $2!,$ $\ldots,$ $99!,$ $100!$ вычеркнуть одно так, чтобы произведение оставшихся оказалось кубом натурального числа? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №35. Точки $D$ и $E$ лежат на продолжениях сторон $AB$ и $BC$ остроугольного треугольника $ABC$ за точки $B$ и $C$ соответственно. Точки $M$ и $N$ — середины отрезков $AE$ и $DC.$ Докажите, что $MN > AD/2.$ ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №36. У Васи Пупкина кончились деньги, и он нанялся на работу. По договору он работал без выходных и за каждый день работы он получал по 100 грошей. Получаемые деньги Вася начал тратить. В первый день работы он потратил 1 грош, а в каждый следующий день тратил на 1 грош больше, чем в предыдущий. К концу какого дня работы Вася снова оказался без денег? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №37. В остроугольном треугольнике $ABC$ угол при вершине $A$ равен 45 градусам. Докажите, что периметр этого треугольника меньше удвоенной суммы его высот, опущенных из вершин $B$ и $C$. ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №38. На столе лежит 101 кучка по 101 спичке. За один ход берется одна спичка из любой кучки. Двое игроков ходят по очереди. Если не позднее 10000-го хода будет взята последняя спичка из какой-то кучки, взявший её выигрывает, иначе — ничья. Может ли кто-то из игроков выиграть независимо от игры соперника, и если да, то кто? ( И. Рубанов, А. Шаповалов )
комментарий/решение(1) олимпиада
Задача №39. Учитель написал на доске 10 отрицательных целых чисел. Вася переписал в тетрадь эти числа, затем записал туда же всевозможные их попарные произведения, всевозможные произведения трёх, четырёх, $\ldots,$ девяти из этих чисел и, наконец, произведение всех десяти чисел. Оказалось, что сумма всех записанных Васей чисел отрицательна. Чему она могла быть равна? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №40. Сумму цифр шестизначного числа умножили на произведение его цифр. Получилось 390. Найдите хотя бы одно такое шестизначное число. ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №41. Петя и Вася стартуют по круговой дорожке из одной точки в направлении против часовой стрелки. Оба бегут с постоянными скоростями, скорость Васи вдвое больше скорости Пети. Петя все время бежит против часовой стрелки, а Вася может менять направление бега, если он перед этим пробежал полкруга или больше в одном направлении. Покажите, что пока Петя бежит первый круг, Вася может трижды, не считая момента старта, поравняться (встретиться или догнать) с ним. ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №42. Найдите все такие пары натуральных чисел $a$ и $b,$ что $\text{НОД}(a, b)+\text{НОК}(a, b) = ab/2.$ ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №43. На шахматной доске $8\times 8$ нарисованы по клеточкам 17 не налегающих друг на друга двухклеточных прямоугольников. Докажите, что на доске найдутся две имеющие общую сторону клетки, одна из которых лежит в одном из нарисованных прямоугольников, а другая — в другом. ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №44. Графики функций $y = k_1x+b_1,$ $y = k_2x+b_2,$ $y = k_3x+b_3$ являются продолжениями сторон равностороннего треугольника. Докажите, что среди чисел $k_1,$ $k_2,$ $k_3$ есть такое, которое не меньше 1/2. ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №45. Игорь нарисовал на клетчатой бумаге со стороной клетки 1 см архипелаг, в котором каждый остров имеет форму многоугольника, составленного из клеток, и разные острова не имеют общих точек. Может ли отношение суммарной длины береговой линии всех островов к их суммарной площади равняться: а) 5; б) 3,99? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №46. Таня и Маша по очереди выписывают на доску натуральные числа, не превосходящие 1000, причем число 13 выписывать нельзя. Начинает Таня. Проигрывает та девочка, после хода которой на доске впервые появятся два одинаковых числа или два числа, отличающиеся на 17. Кто из девочек выиграет при правильной игре, и как ей для этого надо играть? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №47. Прямые $y = ax+b,$ $y = bx+c,$ $y = cx+d,$ $y = dx+a$ ограничивают квадрат. Чему может равняться площадь этого квадрата (укажите все возможности)? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №48. В зашифрованном равенстве АБ+АБ+АБ+АБ+АБ+АБ+АБ+АБ+АБ = ААБ цифры заменены буквами: одинаковые цифры — одной и той же буквой, а разные — разными буквами. Найдите все возможные расшифровки. ( И. Рубанов )
комментарий/решение(2) олимпиада
Задача №49. Дан треугольник $ABC$, в котором $AB = BC$. На стороне $BC$ нашлась такая точка $D$, что $CD = AC$. Точка $E$ на луче $DA$ такова, что $DE = AC$. Какой отрезок длиннее — $EC$ или $AC?$ ( И. Рубанов )
комментарий/решение(2) олимпиада
Задача №50. Найдите все такие тройки положительных чисел $a, b, c,$ что $a+b+c = ab+ac+bc = abc.$ ( И. Рубанов )
комментарий/решение(3) олимпиада
Задача №51. Стороны 100 одинаковых равносторонних треугольников покрашены в 150 цветов так, что в каждый цвет покрашены ровно две стороны. Если приложить два треугольника одноцветными сторонами, то полученный ромб будем называть хорошим. Петя хочет сложить из этих треугольников как можно больше хороших ромбов, причем каждый треугольник должен входить не более, чем в один ромб. Какое наибольшее количество хороших ромбов может гарантировать себе Петя независимо от способа раскраски треугольников? ( И. Рубанов, С. Берлов )
комментарий/решение(1) олимпиада
Задача №52. В 9:00 в путь отправился пешеход. Через час вслед ему из того же начального пункта выехал велосипедист. В 10:30 он догнал пешехода и поехал дальше, но через некоторое время велосипед сломался. Закончив ремонт, велосипедист поехал вслед пешеходу дальше и в 13:00 снова догнал его. Сколько минут занял ремонт? (Скорость пешехода постоянна, и он двигался без остановок, скорость велосипедиста тоже постоянна, и он двигался с единственным перерывом на ремонт.) ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №53. Как без остатка разрезать клетчатый квадрат размером $8\times 8$ клеточек на 10 клетчатых прямоугольников, чтобы все прямоугольники имели различные площади? Все разрезы должны проходить по границам клеточек. ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №54. При каком наибольшем $n$ существует выпуклый $n$-угольник, у которого длины диагоналей принимают не больше двух различных значений? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №55. Можно ли пронумеровать вершины, рёбра и грани куба различными целыми числами от $-12$ до 13 так, чтобы номер каждой вершины равнялся сумме номеров сходящихся в ней рёбер, а номер каждой грани равнялся сумме номеров ограничивающих её рёбер? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №56. Докажите, что для любого целого неотрицательного числа $k$, не превосходящего $\frac{2022\cdot 2021}{2},$ существуют такие 2022 числа, что все их $\frac{2022\cdot 2021}{2}$ попарные суммы различны и среди этих сумм ровно $k$ положительных. (И. Рубанов, С. Берлов, Л. Самойлов) ( И. Рубанов, С. Берлов, Л. Самойлов )
комментарий/решение(1) олимпиада
Задача №57. В каждую клетку таблицы $2012 \times 2012$ вписан либо нуль, либо единица, причем в каждом столбце и каждой строке есть как нули, так и единицы. Докажите, что в этой таблице найдутся две строки и два столбца такие, что на концах одной из диагоналей образованного ими прямоугольника стоят нули, а другой — единицы. ( И. Рубанов, методкомиссия )
комментарий/решение(1) олимпиада
Задача №58. Петя и Вася пробежали одну и ту же дистанцию. Вася бежал вдвое быстрее Пети, но стартовал на минуту позже, и Петя пришёл к финишу первым. Докажите, что Петя пробежал дистанцию меньше чем за две минуты. ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №59. Два числа таковы, что их сумма, сумма их квадратов и сумма их кубов равны одному и тому же числу $m$. Докажите, что сумма четвёртых степеней этих чисел тоже равна $m$. ( И. Рубанов )
комментарий/решение(2) олимпиада
Задача №60. В треугольнике $ABC$ провели биссектрису $BE$ и серединный перпендикуляр $m$ к стороне $AB$. Оказалось, что $BE = EC$, а прямая $m$ пересекает сторону $BC$. Докажите, что угол $C$ меньше 36 градусов. ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №61. Из нечётных натуральных чисел от 1 до 47 составили 12 дробей, меньших 1, использовав каждое число по одному разу. Получившиеся дроби разбили на группы равных между собой. Какое наименьшее количество групп могло получиться? ( И. Рубанов )
комментарий/решение(2) олимпиада
Задача №62. Запишите четыре числа (не обязательно целых), среди которых нет одинаковых, чтобы выполнялось такое условие: если число $x$ есть среди записанных, то хотя бы одно из чисел $x-1$ или $6x-1$ тоже есть среди записанных. ( И. Рубанов, С. Берлов )
комментарий/решение(2) олимпиада
Задача №63. Внутри стороны $BC$ выпуклого четырехугольника $ABCD$ нашлась такая точка $E$, что прямая $AE$ делит четырёхугольник на две равные по площади части. Какая из вершин четырехугольника находится дальше всех от прямой $AE$? ( И. Рубанов, Д. Ширяев )
комментарий/решение(3) олимпиада
Задача №64. Петя и Вася играют в такую игру. Вначале в каждой из 2022 коробок лежит по одной спичке. За один ход можно переложить все спички из любой непустой коробки в любую другую непустую коробку. Ходят по очереди, начинает Петя. Побеждает тот, после хода которого в какой-то коробке впервые окажется не меньше половины всех спичек. Кто победит при правильной игре? ( И. Рубанов )
комментарий/решение(12) олимпиада
Задача №65. Вася расставил по кругу все натуральные числа от 1 до 100 в каком-то порядке. Скажем, что число хорошо стоит, если соседнее с ним число по часовой стрелке больше, чем соседнее с ним число против часовой стрелки. Могло ли оказаться, что хорошо стоят по крайней мере 99 чисел? ( И. Рубанов, А. Голованов )
комментарий/решение(1) олимпиада
Задача №66. На клетчатую доску размером $100\times 100$ поставили 1975 ладей (каждая ладья занимает одну клетку, разные ладьи стоят на разных клетках). Какое наибольшее количество пар ладей, бьющих друг друга, могло при этом получиться? Напомним, что ладья может бить на любое число клеток по горизонтали и вертикали, но не бьёт ладью, загороженную другой ладьёй. ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №67. На тренировке спортсмен преодолел 60 км за 3,5 часа. Сначала он плыл со скоростью 8 км/ч, потом бежал со скоростью 16 км/ч, а затем ехал на велосипеде со скоростью 24 км/ч. Что он делал дольше — плыл или ехал на велосипеде? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №68. В треугольнике $ABC$, у которого угол $B$ меньше 120 градусов, медиана $BD$ короче половины стороны $AB$. Докажите, что эта медиана длиннее половины стороны $BC$. ( И. Рубанов )
комментарий/решение(2) олимпиада
Задача №69. Существуют ли такие 2022 натуральных числа, что среди них нет одинаковых и произведение любых 1012 из них делится на произведение остальных 1010? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №70. В белом клетчатом квадрате размером $10\times 10$ клеток закрасили черным 84 клетки. Какое наименьшее количество «уголков» из трех черных клеток могло при этом образоваться? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №71. Маша взяла четыре различных положительных числа и записала шесть их попарных произведений в ряд в порядке возрастания. Могли ли все пять разностей между соседними числами этого ряда оказаться одинаковыми? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №72. Два бегуна бегают с равными постоянными скоростями по диагоналям $AC$ и $BD$ соответственно квадрата $ABCD.$ Добежав до конца диагонали, бегун сразу поворачивает обратно. Стартовали они одновременно из двух случайно выбранных точек своих диагоналей. Докажите, что найдётся момент, когда расстояние между бегунами будет строго меньше половины диагонали квадрата. ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №73. Пусть $p_1$, $p_2$, $\ldots$, $p_{100}$ — сто простых чисел, среди которых нет одинаковых. Натуральные числа $a_1$, $\ldots$, $a_k,$ большие 1, таковы, что каждое из чисел $p_1p_2^3$, $p_2p_3^3$, $\ldots$, $p_{99}p_{100}^3$, ${p_{100}}p_1^3$ равно произведению каких-то двух из чисел $a_1$, $\ldots$, $a_k.$ Докажите, что $k \ge 150$. ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №74. Назовем пару различных натуральных чисел хорошей, если одно из них делится на другое. Найдите такие 20 натуральных чисел, среди которых нет равных, что если выписать все возможные пары этих чисел, то количество хороших среди них будет равно 101. (Каждая пара записывается один раз. Порядок чисел в парах не учитывается, то есть пары ${(a, b)}$ и ${(b, a)}$ считаются за одну.)
Не забудьте объяснить, почему найденные вами числа действительно дают ровно 101 хорошую пару, не больше и не меньше. Ответы без объяснения не засчитываются. ( И. Рубанов, С. Берлов )
комментарий/решение(1) олимпиада
Задача №75. Пять положительных чисел таковы, что сумма их кубов меньше суммы их квадратов. Докажите, что каждое из этих чисел меньше 2. ( И. Рубанов )
комментарий/решение(3) олимпиада
Задача №76. При каких натуральных $n$, больших 5, клетчатый квадрат размером $n\times n$ клеточек можно без остатка разрезать на прямоугольники из двух клеток и кресты из пяти клеток так, чтобы получились фигуры обоих этих видов? Крест из пяти клеток изображен на рисунке справа. ( И. Рубанов )
комментарий/решение(6) олимпиада
Задача №77. У натурального числа стерли две последние цифры и полученное число прибавили к исходному. Могло ли в сумме получиться число $101^{50}-1$? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №78. Петя, Вася и Коля бежали по кольцевой дорожке с постоянными скоростями в одном направлении. Они стартовали одновременно и из одной точки. Петя впервые обогнал Васю на своем четвертом круге (то есть пробежав больше трех кругов, но еще не закончив четвертый), а Колю — на своем седьмом круге. Докажите, что Коля впервые обогнал Васю раньше, чем пробежал десять кругов. ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №79. Вася отметил невидимыми чернилами одну из клеток таблицы размером $5\times 5$ клеток. Разрешается выделить в таблице четыре идущих подряд по горизонтали или вертикали клетки и спросить у Васи, есть ли среди них отмеченная. Каждый следующий вопрос задается после ответа на предыдущий. За какое наименьшее количество таких вопросов можно наверняка определить отмеченную клетку? ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №80. Три числа таковы, что куб суммы любых двух из них равен сумме их кубов. Докажите, что среди этих чисел есть нуль. ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №81. Шестиугольник, все углы которого меньше 180 градусов, таков, что каждый треугольник, образованный тремя идущими подряд его вершинами, имеет площадь 1. Докажите, что площадь этого шестиугольника не меньше 6. ( И. Рубанов )
комментарий/решение(1) олимпиада
Задача №82. Звезда состоит из 100 горючих шнуров $OA_1$, $\ldots$, $OA_{100}$, соединенных в единственной точке $O$. Время горения каждого шнура не зависит от того, с какого конца его поджигают, а скорость горения не обязана быть постоянной. Если поджечь звезду в точке $A_1$, она полностью сгорит за 201 секунду, если в точке $A_2$ — за 202 секунды, $\ldots$, если в точке $A_{99}$ — за 299 секунд. За какое время звезда полностью сгорит, если ее поджечь в точке $A_{100}$? ( И. Рубанов )
комментарий/решение(2) олимпиада